
BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
Ein Bayes'sches Netz besteht aus einem Graph und bedingten Wahrscheinlichkeitsverteilungen:
- Der Graph enthält Knoten, die Zufallsvariablen im Bayes'schen Sinne repräsentieren, sowie Kanten zwischen den Knoten, die (direkte) kausale Abhängigkeiten darstellen.
- Die Kanten im Graph sind gerichtet und stellen damit jeweils einen kausalen Einfluss vom Knoten an dem die Kante beginnt (der Ursache) auf den Knoten auf den die Kante verweist (der Wirkung) dar.
Das schließt jedoch nicht aus, dass es mehrere Wege von einem Knoten A zu einem Knoten B geben kann, es wird also keine Baumstruktur vorausgesetzt.
Auch muss nicht verlangt werden, dass es zwischen je zwei Knoten mindestens eine Verbindung (ungeachtet der Kantenrichtung) gibt, also der Graph verbunden (connected) ist. Da unverbundene Teilgraphen jedoch in jeder Hinsicht vollkommen unabhängig voneinander sind, ist es für die weitere Betrachtung einfacher solche unverbundenen Teilgraphen gleich als vollkommen eigenständige Netze zu betrachten. Es wird hier also im Weiteren von Verbundenen Graphen ausgegangen bei denen es zwischen je zwei Knoten A und B mindestens einen ("ungerichteten") Pfad von A nach B gibt, wobei dieser Pfad die Kantenrichtung nicht beachtet (z.B. gibt es im unten gezeigten Netz einen ungerichteten Pfad von "Unfälle" nach "Wetter" über "Sicht").
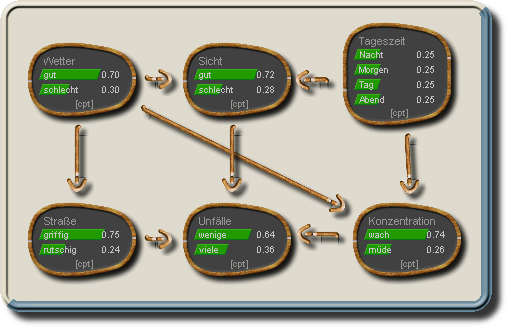
Beispiel-Netz
Durch die Graphen-Struktur hat jeder Knoten A eine Menge von Elternknoten pa(A). Diese umfasst all jene Knoten von denen eine Kante ausgeht, die auf den Knoten A zeigt. Dieser Satz von Elternknoten kann auch leer sein (pa(A)={}), was in einem DAG auch für mindestens einen Knoten der Fall sein muss. Entsprechendes gilt auch für die Menge der Kindknoten ch(A), also jene Knoten zu denen von A ausgehend eine Kante führt.1)
Für jeden Knoten X im DAG
müssen dann bedingte
Wahrscheinlichkeitsverteilungen p(X|pa(X))
für den Knoten gegeben seine Eltern pa(X)
definiert werden. Im Falle der häufig gemachten
Einschränkung auf kategoriale Variablen haben
diese Wahrscheinlichkeitsverteilungen die Form (mehrdimensionaler)
Tafeln (CPTs). Für
Variablen mit einer kontinuierlichen Zustandsmenge
würden (mehrdimensionale) Dichteverteilungen
benötigt. Dabei müssen aber mehrere
Einschränkungen gemacht werden, die hier nicht weiter
erläutert werden (siehe dazu den Abschnitt
zu kontinuierlichen und hybriden Netzen). Für elternlose
Knoten wird die sogenannte a-priori-Verteilung p(X)
verlangt (die für diskrete Knoten verallgemeinert
ebenfalls als CPT bezeichnet wird).
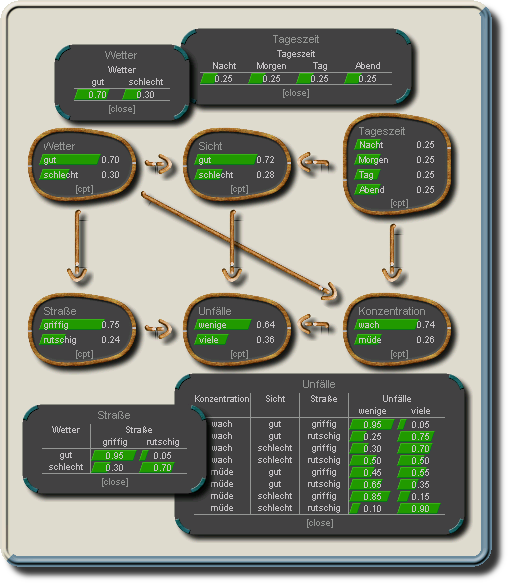
Beispiel-Netz mit bedingten Wahrscheinlichkeiten (für einige der Knoten).
Für elternlose Knoten werden die A-Priori-Wahrscheinlichkeiten gegeben.
Weiterreichende Abhängigkeiten zwischen Knoten können je nachdem über welche Knoten man Wissen aufgrund von Beobachtungen erlangt hat blockiert werden oder auch erst entstehen. Knoten deren Zustand bekannt ist werden als "gegeben" bezeichnet.
Es gilt:
Ein Knoten gegeben die Zustände seiner Elternknoten ist unabhängig von allen (sonstigen) Nicht-Nachfahren (das sind u.a. alle Vorfahren, da durch die Bedingungen an ein DAG ein Vorfahre nicht auch ein Nachfahre sein kann ohne einen gerichteten Zyklus zu erzeugen)Für komplexere Unabhängigkeitsverhältnisse ist die Beschreibung mit Hilfe der d-separation / d-connection [1] hilfreicher:
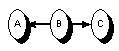 |
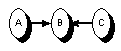 |
|
| serielle Verbindung | divergierende Verbindung | konvergierende Verbindung |
Zwei Knoten A und B sind abhängig (d-connected) gegeben die aktuellen Beobachtungen, wenn es einen Pfad von A nach B gibt für den gilt:Gibt es keinen solchen Pfad sind A und B d-separiert, d.h. unabhängig gegeben die aktuellen Beobachtungen. Die Stärke der Abhängigkeiten hängt von den Werten der bedingten Wahrscheinlichkeitstafeln ab. Diese können im Extremfall auch so gewählt sein, dass zwei Knoten obwohl d-connected dennoch tatsächlich unabhängig sind.1)
- Der Pfad enthält keine serielle oder divergierende Verbindung bei der der Zustand des mittleren Knotens (Knoten B in obigen Beispielen) beobachtet wurde - d.h. gegeben ist
- Für die mittleren Knoten aller konvergierenden Verbindungen des Pfads liegt Information vor, entweder indem der Knoten direkt gegeben ist oder indem einer seiner Nachfolger bekannt ist.
| 1) | Das ist z.B. immer der Fall wenn eine Gleichverteilung in allen Wahrscheinlichkeitstafeln hinterlegt wird. |
Die einfachste, jedoch nur in sehr einfachen Netzen praktikable Möglichkeit dieses zu tun besteht darin, zunächst die Verbundwahrscheinlichkeitstafel aller Knoten über die Kettenregel zu bestimmen (s.a. Rechenregeln):
|
P(X1,...,XZ) =
|
|
P(Xi|pa(Xi)) |
|
|
In dieser Tafel sind dann alle durch Beobachtung
ausgeschlossenen Zustandskombinationen auf 0 zu setzen und
die so gewonnene Tafel P* zu renormieren (so dass
die Gesamtsumme aller Werte wieder 1 ergibt):
|
P'(X1,...,XZ) = P*(X1,...,XZ) /
|
|
P*(X1,...,XZ) |
|
|
Aus der Tafel P' können dann die A-Posteriori-Wahrscheinlichkeitsverteilungen
marginalisiert werden z.B. für den Knoten X
durch:
|
P'(X)
=
|
|
P'(X1,...,XZ) |
|
|
Leider ist eine Verbundtafel aller Knoten in nicht trivialen Netzen viel zu groß um damit effizient (oder überhaupt) rechnen zu können. Eine Lösung ergibt sich durch das ganz normale Distributivgesetz von Addition und Multiplikation (ab+ac = a(b+c)). Daraus folgt, dass abhängig von der Netzstruktur bereits bestimmte nicht mehr vorkommende Merkmale aus Zwischenergebnissen der Kettenregel "herausmarginalisiert" werden können. Leider ist dieses Verfahren abhängig davon für welches Merkmal die A-Posteriori-Verteilung berechnet werden soll, d.h. um alle unbekannten Knoten zu bestimmen muss mehrfach gerechnet werden.
Trotzdem lässt sich aus diesem Grundgedanken auch eine Methode ableiten, die auch dieses Problem löst. Dazu wird das Netz in mehreren Schritten in eine andere Form überführt, die es schließlich gestattet effizient aus der beobachteten Information bezüglich einzelner Variablen (Evidenz) Rückschlüsse auf die resultierenden Wahrscheinlichkeits-Verteilungen (A-Posteriori-Wahrscheinlichkeiten) der übrigen unbekannten Merkmale zu ziehen. Dieses Verfahren bestimmt zunächst eigentlich eine möglichst optimale Abfolge der Marginalisierungen, was durch ein graphisches Verfahren geschieht.
Dabei wird zunächst der sogenannte Moralische Graph aus dem DAG gebildet, indem für jeden Knoten X alle Eltern pa(X) paarweise durch ungerichtete Kanten verbunden werden (wenn sie noch nicht verbunden sind) und die gerichteten Kanten in ungerichtete Kanten überführt werden (einfach durch das Vernachlässigen der Richtung).
Ein weiterer Graph, der aus dem Moralischen Graph erzeugt wird ist der Triangulierte (Moralische) Graph.
- Ein Graph ist trianguliert, wenn jeder (ungerichtete) zyklische Pfad mit mehr als drei Knoten eine direkte Abkürzung (ohne Zwischenstationen) enthält.
- Cliquen sind die größten maximal verbundenen Teilgraphen eines triangulierten Graphen.
- Maximal verbunden ist ein (Teil-)Graph wenn alle seine Knoten paarweise verbunden sind, d.h. keine Kante "fehlt".
- Größter maximal verbundener Teilgraph heißt ein Teilgraph dann, wenn ihm kein weiterer Knoten hinzugerechnet werden kann, ohne dass das Maximal-Verbunden-Kriterium gebrochen würde.
Zur Triangulierung und Cliquen-Bestimmung
kann der Eliminierungs-Algorithmus[1] verwendet werden:
- Wähle einen Knoten X
- Verbinde paarweise alle Nachbarn von X durch eine Kante (wenn noch nicht verbunden)
- Sofern X und alle Nachbarn von X nicht schon Teil einer zuvor gefundenen Clique sind bilden sie eine neue Clique
- Entferne (eliminiere) X
- Wiederhole die Schritte 1-4 bis kein Knoten mehr übrig ist.
Dieses Verfahren sorgt u.a. auch dafür dass es für jeden Knoten X mindestens eine Clique gibt die sowohl X selbst als auch alle Elternknoten pa(X) enthält. Eine solche Clique wird als Home-Clique bezeichnet.
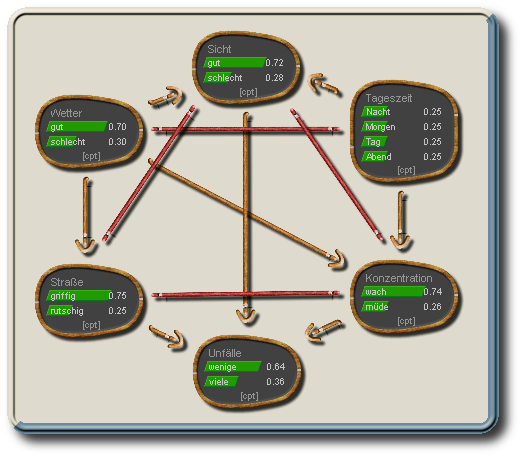
Triangulierter Moralischer Graph
Dieser Graph ist bereits durch die zusätzlichen Kanten zur "Moralisierung" (Verheiratung von Elternknoten gemeinsamer Kindknoten) auch trianguliert, ohne dass noch zusätzliche "Fill-Ins" eingefügt werden müssen.
Aus den Cliquen wird eine sekundäre Struktur, der Junction-Tree erzeugt. Im Junction-Tree bilden die Cliquen die (Hyper-)Knoten, während die Separatoren die Kanten darstellen.
Die Cliquen müssen durch Separatoren derart verbunden werden, dass eine Baum-Struktur gebildet wird, die zusätzlich die Running-Intersection-Eigenschaft erfüllt (d.h. es werden i.d.R. nicht alle denkbaren Separatoren verwendet).- Ein Graph ist verbunden (connected), wenn es zwischen je zwei Knoten mindestens einen Pfad gibt
- Eine verbundener Graph mit Z Knoten und Z-1 Kanten heißt Baum. In einem Baum sind alle Knoten über genau einen Pfad verbunden.
- Die Running-Intersection-Eigenschaft ist dann erfüllt, wenn ein Knoten, der in zwei Cliquen auftritt auch in jeder Clique des (einzigen) Pfads zwischen diesen beiden Cliquen vorkommt (und damit auch in jedem Separator dieses Pfads). Dieses ist nur in triangulierten Graphen möglich.
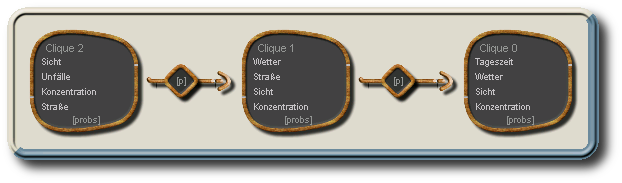
Junction-Tree mit 3 Cliquen und 2 Separatoren (die enthaltenen Knoten sind hier nur für die Cliquen dargestellt), wie er mit folgender Eliminierungsreihenfolge entsteht: Tageszeit, Wetter, Sicht, Konzentration, Straße, Unfälle, wobei für die letzten drei Knoten keine Cliquen entstehen, da diese jeweils Teilmenge mind. einer anderen Cliquen wären.
Zu Cliquen, wie auch Separatoren werden dann die zugehörigen Wahrscheinlichkeitstafeln aufgestellt (s. Initialisierung) . Diese bestehen aus den Verbundwahrscheinlichkeiten (nicht mehr den bedingten Wahrscheinlichkeiten) der enthaltenen Knoten. Evidenz wird von Clique zu Clique über die Separatorentafeln weitergeleitet, um die vorhandene Information über den gesamten Junction-Tree zu propagieren und die resultierenden A-Posteriori-Wahrscheinlichkeitsverteilungen aller Knoten zu gewinnen. Es existieren verschiedene Propagations-Methoden, die einen Junction-Tree benutzen.
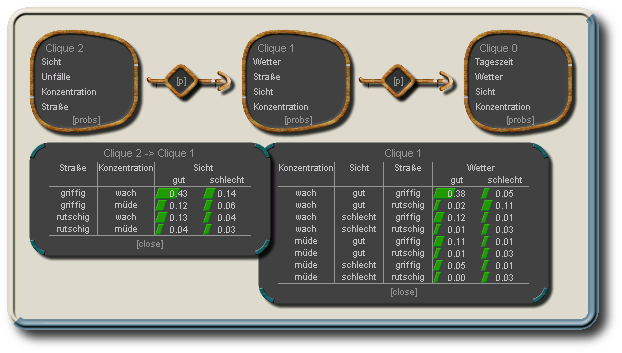
Verbundwahrscheinlichkeitstafeln für Clique 1 (unten rechts) und den Separator zwischen Clique 1 und Clique 2 (unten links) des Junction-Trees (nach Initialisierung und Propagation ohne Evidenz)
Ein Beispiel ist die HUGIN-Propagation [1]. Zunächst wird die Evidenz in den Junction-Tree eingebracht, indem Zellen die mit unmöglichen Zuständen korrespondieren auf 0 gesetzt werden. Das geschieht für jeden Knoten (mit Evidenz) in einer beliebigen, diesen Knoten enthaltenden Cliquen Tafel. Nachdem alle verfügbare Evidenz eingebracht ist, muss die Information über den gesamten Junction-Tree propagiert werden. Um Information von einer Clique C1 über einen Separator S zu einer Clique C2 weiterzuleiten wird folgendes Berechnungs-Schema verwendet:
| P(C2') := |
|
|
|
|
||
|
P(S') :=
|
|
P(C1) |
|
|
||
|
|
||
| P(S) := |
|
P(C2) |
|
|
||
Dabei sind:
- P(C1) und P(C2) die beiden Cliquen-Tafeln (vor der Informationsweiterleitung),
- P(S) ist die "alte" Separator-Tafel, die der Randwahrscheinlichkeit für S aus P(C2) entspricht und
- P(S') ist die neue Tafel die die weiterzuleitende Information aus P(C1) enthält.
- P(C2') schließlich ist die neue Cliquentafel der Clique C2.
Die initialen Verbundwahrscheinlichkeiten zu den Cliquen und Separatoren werden durch folgendes Verfahren gewonnen:
- Alle Cliquen- und Separatorentafeln werden mit 1 initialisiert
- Die bedingte Wahrscheinlichkeitstafel jedes Knotens wird in eine Home-Clique dieses Knotens einmultipliziert
- Nach einer vollständigen Propagation (Collect- und Distribute-Phase) ist der Junction-Tree initialisiert, d.h. die Verbundtafeln der Cliquen und Separatoren wurden erzeugt.
Hauptproblem aller exakten Berechnungsverfahren ist das Finden eines handhabbaren Junction-Trees. Diese Frage hängt auch mit der Triangulierung zusammen. Es ist nicht zu gewährleisten, dass hierfür eine optimale Lösung (in annehmbarer Zeit) gefunden werden kann. Es gibt jedoch auch Netzstrukturen für die selbst der optimale Junction-Tree noch zu komplex ist um mit ihm effektiv rechnen zu können. Neben der exakten Berechnung über einen Junction-Tree existieren daher auch noch approximative Verfahren. Diese schätzen die Verteilungen indem eine Anzahl von möglichen Beispielen (Samples) entsprechend der durch das Netz vorgegebenen Wahrscheinlichkeitsverteilungen erzeugt wird (Monte Carlo Sampling) (s.a. BN's und Daten).
Grundlage der Wahrscheinlichkeitsrechnung sind die Axiome vom Kolmogorov:
Axiom I: Die Wahrscheinlichkeitsfunktion P(.) ordnet jedem Ereignis x aus einer Ereignismenge W ("Omega") einen Wert zwischen 0 und 1 zu.0 <= P(x) <= 1
Axiom II: W ("Omega") ist das sichere Ereignis, es gilt:P(W) = 1
Axiom III: für zwei disjunkte (sich gegenseitig ausschließende) Ereignisse a und b gilt:P(a or b) = P(a) + P(b)
Es gilt für die hier gemachten Berechnungen die Setzung:
0 / 0 := 0
Dies wird benötigt, da der Fall "0/0" z.B. in der Informationweiterleitung für durch Beobachtung ausgeschlossene Zustände auftritt (dabei soll es einfach bei "unmöglich" also P(.)=0 bleiben).
Die Multiplikation /
Division / Addition / Subtraktion zweier
Wahrscheinlichkeits-Tafeln ergibt eine Tafel die (formal)
die Vereinigungsmenge der Merkmale beider Tafeln
enthält:
| P(A,B) |
|
P(B,C) | = | P(A,B,C) | mit | P(a,b,c) | = | P(a,b) | op | P(b,c) |
Dabei
- steht op für den jeweiligen Operator aus {*, /, +, -}
- gehen a,b,c über alle Kombinationen der Indizes der Zustände von A,B und C
Marginalisierung "entfernt"
Merkmale
aus einer Tafel, indem über alle Werte, die sich nur in
den Zuständen der zu marginalisierenden Merkmale
unterscheiden summiert wird.
|
|
|
||||||
|
|
|
|
|
|
|
|
P(a,b,c,d) |
|
|
|
|
Dabei
- sind #C bzw. #D die Anzahl der Zustände des Merkmals C bzw. D
- und a,b nehmen alle Zustandskombinationen der Merkmale A und B an.

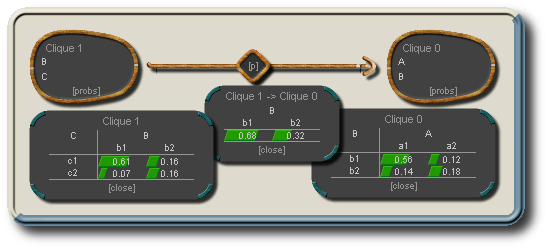
Junction-Tree zum obigen Beispiel mit zwei Cliquen (B,C) und (A,B), einem Separator (B) und den zugehörigen Verbundwahrscheinlichkeiten:
Nun, Frösche haben ja bekanntlich die Fähigkeit das Wetter - also praktisch den Urquell aller Unsicherheit - vorherzusagen. Das ist etwas, was zugegebenermaßen auch mit Bayes'schen Netzen (noch) nicht wirklich möglich ist - aber man wird ja noch träumen dürfen. Ok, normalerweise sagt einem der Anblick einer übel gelaunten Kröte auch nichts, was man nicht durch einen Blick aus dem Fenster selbst rausgekriegt hätte, ... aber prinzipiell könnten sie wenn sie nur mal wollten (und nicht ständig so üble Laune hätten)...
- Zum Kapitel über die Decomposition Bayes'scher Netze (triangulieren von Graphen)
- Zum Kapitel
über Dynamische Bayes'sche Netze
(zur Zeitreihenuntersuchung) - Zum
Kapitel über Modulare Bayes'sche Netze
(Module statisch / dynamisch zusammenfügen) - Zum Kapitel
über Bayes'sche Netze & Daten
(Struktur und bed. Wahrscheinlichkeiten aus Daten ableiten / Klassifikation / Daten-Sampling) - Zum
Kapitel über Kontinuierliche und Hybride Netze
(Netze mit Knoten mit kontinuierlichen Wertebereichen) - Zu den
(statischen) Anwendungs-Beispielen
(Explaining Away, Soft Evidence, Simpson Paradox, ...) - Für Safari, Google-Chrome und Mozilla-Browser
(Firefox, Seamonkey), sowie mit Einschränkungen auch
mit Opera1)
nutzbar jetzt auch verschiedene interaktive
Online-Beispiele (alle noch Beta):
- Anwendungs-Beispiele
(Explaining Away, Soft Evidence, Simpson Paradox, Hidden-Markov-Models, ...) - Verschiedene
Inferenz-Algorithmen
(Full-Joint, Junction-Tree, Loopy-Belief, LW-Sampling, Gibbs-Sampling) - Max-Propagation
(Full-Joint, Junction-Tree, Loopy-Belief) - Dynamische Netze
(d-HUGUN) - Lern-Algorithmen
(Lernen der bedingten Wahrscheinlichkeiten, Lernen der Struktur) - Hybride Netze
(Semi-Strong-Elimination-Tree, LW-Sampling) - Größere
Beispielnetze
(bekannte Beispiele)
- Optimierung der
Triangulierung (Tree-Decomposition)
(mit Evolutionären Algorithmen)
| 1) | Kanten werden nicht richtig dargestellt. |
| 1) | Funktioniert nur mit neueren Safari-, Google-Chrome- oder Mozilla-Browsern (Firefox, SeaMonkey), sowie mit Einschränkungen auch mit Opera. |
 .
.