
BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
1) |
||
2) |
3)
 |
|
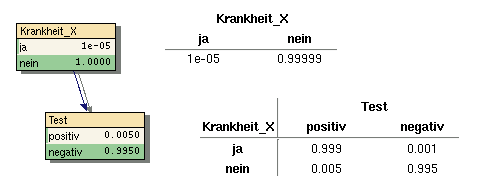
Sehr anschaulich darstellen lässt sich das bayes'sche Schließen am einfachen Beispiel einer Krankheit "X", zu deren Diagnose ein Test existiert. Dabei ist das Testergebnis kausal davon abhängig ob die Krankheit vorliegt oder nicht (sicher nicht umgekehrt).
- Die Krankheit ist sehr selten: nur ein Mensch von 100000 hat sie (siehe a-priori-Wahrscheinlichkeit im Knoten Krankheit_X in Bild 1).
- Wenn ein Patient die Krankheit hat, dann fällt der Test in 99.9% der Fälle positiv aus - in 0.1% der Fälle dagegen fälschlicher Weise negativ (Missing) (siehe Test gegeben Krankheit_X=ja in Bild 2).
- Wenn ein Patient die Krankheit nicht hat, dann ist das Testergebnis in 99.5% der Fälle negativ, in 0.5% der Fälle gibt es einen "Falschalarm" (false alarm) (Krankheit_X=nein, Bild 3)
4) |
5) |
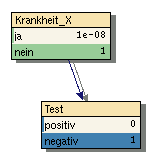
Interessanter sowohl für dieses Beispiel als auch in "Real-Life" ist nun umgekehrt vom Ausgang des Tests auf die Erkrankung zu schließen.
- Wenn der Test negativ ausfällt, dann ist die Wahrscheinlichkeit trotzdem die Krankheit zu haben mit 0.000001% extrem klein (Bild 4)
- Wenn der Test anschlägt, dann ist liegt die Wahrscheinlichkeit tatsächlich an "X" erkrankt zu sein trotzdem nur bei 0.2% (Bild 5)
Um die Ergebnisse dieses Modells nachzurechnen reicht die Bayes'sche Formel:
| P(A|B) = |
|
|
|
|
||
|
P(B)
=
|
|
P(B|A) P(A) |
|
|
||
Erst recht bei komplizierteren Zusammenhängen (reale BN's z.B. im medizinischen Bereich haben z.T. hunderte von Merkmalen) rechtfertigt sich die Anwendung von BN's, die zum einen ihr "Wissen" intuitiv verständlich in der Form eines Graphen (globales Wissen) und zum anderen durch bedingte Wahrscheinlichkeiten in Abhängigkeit von den direkten Ursachen (lokales Wissen) repräsentieren. Damit sind BN's kein Black-Box-Verfahren, sondern ermöglichen die Kombination von Expertenwissen und Datenauswertungen (Lernverfahren).
6) |
7) |
8)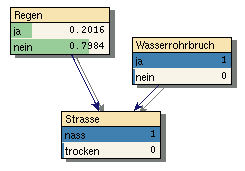 |
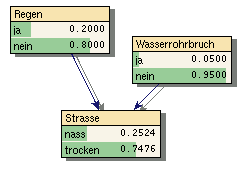
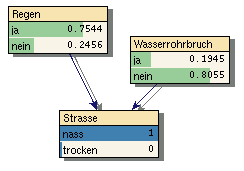
Das Rechnen in Wahrscheinlichkeiten gewährleistet die innere Konsistenz der Verfahren. Sehr gut abgebildet wird z.B. der Explaining-Away-Effekt. Im obigen Beispiel führt die Beobachtung, dass die Straße nass ist zunächst dazu dass beide Ursachen Regen und Wasserrohrbruch an Wahrscheinlichkeit zunehmen (vgl. Bild 6 und 7). Im zweiten Schritt wird aber zusätzlich bekannt, dass es tatsächlich einen Wasserrohrbruch gegeben hat, wodurch die Wahrscheinlichkeit für Regen annähernd wieder auf die A-Priori-Wahrscheinlichkeit von 20% sinkt (Bild 8).
9)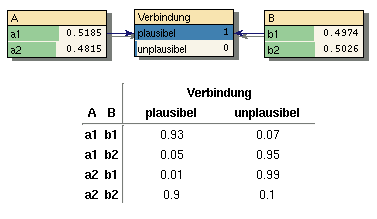 |
Ein Problem in der Modellierung von BN's ist die
Kausalitätsannahme, die nicht immer zutreffend ist. Es müsste
auch ungerichtete Verbindungen geben, die keine
Ursache-Wirkung-Beziehung darstellen. Dies ist nur mit einem
kleinen Trick zu realisieren:
Zwei Knoten A und B, die in einer solchen
ungerichteten
Beziehung stehen erhalten einen gemeinsamen Kindknoten. Dieser hat zwei
Zustände,
hier plausibel und unplausibel genannt. Alle
plausiblen / unplausiblen
Zustandskombinationen der Knoten A und B
sprechen
für den jeweiligen Zustand des Verbindungsknoten. Im gezeigten
Beispiel
wurden z.B. die Kombinationen a1,b1 und a2,b2 als
plausibel
angenommen während a1,b2 und a2,b1 unplausibel
sind.
Der Verbindungsknoten wird immer als Verbindung=plausibel
instanziiert,
so dass damit die gewünschte Abhängigkeit zwischen A
und B hergestellt ist
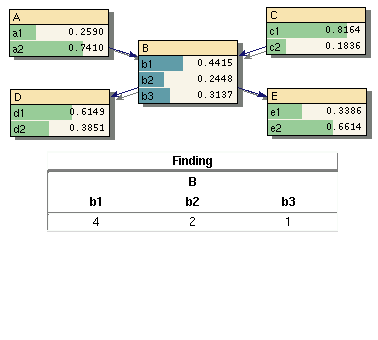 |
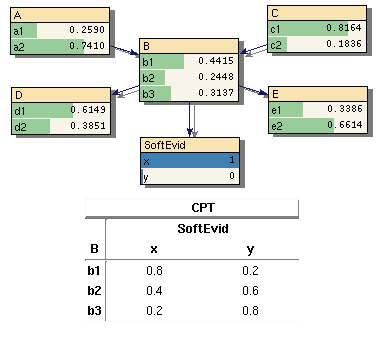 |
Neben Beobachtungen der Art, dass ein einziger Zustand eines Merkmals mit Sicherheit bekannt ist (hard Evidence), kann es auch unsichere Information (soft Evidence) geben.
- Diese kann z.B. bei einem Merkmal mit mehr als zwei Zuständen einen oder mehrere mit Sicherheit ausschließen, wobei aber noch mehr als ein Zustand möglich bleibt, oder
- es kann ein subjektiver Glauben ausgedrückt werden, dass ein Zustand eher anzunehmen ist als ein anderer.
- Eine "0" schließt den Zustand mit Sicherheit aus
- Werte >0 geben in Relation zueinander die Stärke des subjektiven Glaubens an (Bild 10).
- Für harte Evidenz und wenn nur Zustände ausgeschlossen werden sollen enthält der Finding-Vektor nur die Werte "0" und "1".
- serielle und divergierende Verbindungen werden nicht d-separiert,
- konvergierende Verbindungen jedoch d-connected.
12)
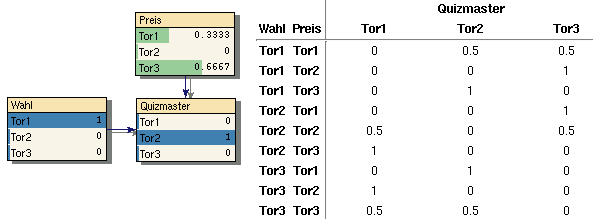
Ein nettes Beispiel, über das (angeblich) selbst Mathe-Profs miteinander in die Wolle geraten sind ist dieses: Ein Kandidat hat die Wahl zwischen drei verschlossenen Toren. Hinter einem verbirgt sich ein Preis, hinter den andern beiden sind Nieten ("Zonks"). Nachdem der Kandidat ein Tor gewählt hat öffnet der Quizmaster eines der beiden anderen Tore und zwar eines hinter dem sich der Preis nicht befindet (der Quizmaster weiß also wo der Preis ist). Nun erhält der Kandidat noch einmal die Chance sich umzuentscheiden also das andere noch nicht geöffnete Tor zu nehmen. Die Frage lautet nun: Ist es sinnvoller die erste Entscheidung zu ändern oder sie beizubehalten? Bild 12 zeigt das BN zu dieser Fragestellung. Die CPT für den Knoten (welches Tor öffnet der) Quizmaster ist dargestellt. Die anderen beiden CPT's enthalten die A-Priori-Wahrscheinlichkeiten für die Wahl (des Kandidaten) und (wo ist der) Preis. Diese liegen jeweils bei 1/3 für jedes Tor. Hier ist das Ergebnis gezeigt, wenn der Kandidat zunächst Tor1 wählt und der Quizmaster dann Tor2 öffnet. Es zeigt sich, dass es sinnvoll ist zu wechseln, da die Wahrscheinlichkeit dass sich der Preis hinter Tor3 befindet nun bei 2/3 zu 1/3 für Tor1 liegt. Alle übrigen möglichen Fälle liefern dasselbe Resultat: Man verdoppelt die Gewinnchanchen, wenn man immer die erste Wahl ändert. Das Beispiel zeigt nochmals wie ein Ergebnis auf das nicht jeder ohne Weiteres kommt mit Hilfe eines BN's berechnet werden kann, das wohl (fast) jeder hätte aufstellen können.
13)
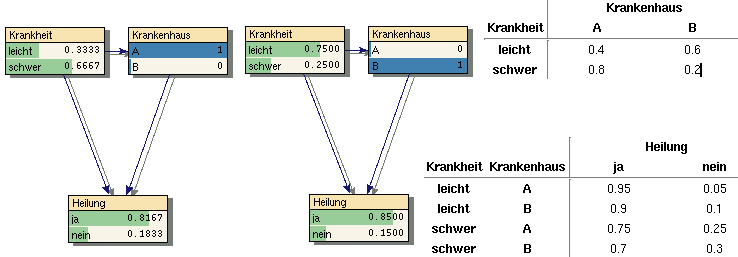
Das sogenannte Simpson-Paradox hat schon in einigen realen - teils recht makabren - Fällen zu (gewollter) Fehlinformation geführt. Auch das in Bild 13 gezeigte Beispiel ist an einen realen Fall angelehnt - allerdings startk vereinfacht. Die Frage ist: Wo sind die Heilungs-Chancen besser - in Krankenhaus A oder in Krankenhaus B? Links ist als Evidenz Krankenhaus=A angegeben, rechts Krankenhaus=B. Man sieht, dass die Chancen in Krankenhaus B mit 85% besser stehen als in Krankenhaus A (81.67%). Also in welches Krankenhaus würde man gehen wenn man die Wahl hat? Krankenhaus B? Besser nicht! Die CPT des Merkmals Heilung (rechts unten) die zusätzlich nach der Schwere der Krankheit aufgeschlüsselt ist zeigt deutlich, dass die Chancen sowohl von leichten als auch von schweren Krankheiten geheilt zu werden in Krankenhaus A jeweils 5% besser liegen! Der Effekt rührt daher, dass schwer Kranke eher in Krankenhaus A, leichter Erkrankte eher in Krankenhaus B landen (siehe CPT des Merkmals Krankenhaus; rechts oben). Einfach gesagt: In Krankenhaus A sind mehr schwer Kranke, die die Gesamt-Heilungs-Chancen nach unten ziehen.