TUTORIAL:
BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
Die bisherigen Ausführungen
bezogen sich implizit oder explizit alle auf den "Normalfall"
Bayes'scher Netze, also solche Netze mit ausschließlich
diskreten Knoten. Diskrete Knoten haben eine relativ kleine,
in jedem Fall aber endliche Menge von (sich gegenseitig
ausschließenden) Zuständen, die man auch Kategorien
nennen kann. Beispiele dafür sind Kategorien wie
"ja"/"nein", "klein"/"mittel"/"hoch", "blond"/"intelligent"
(kleiner Scherz :-), usw. Die Wahrscheinlichkeitsverteilungen
solcher Knoten (Variablen) lassen sich in der Form von
(mehrdimensionalen) Tabellen abbilden, welche
Wahrscheinlichkeitswerte (also Zahlen im Bereich [0...1])
enthalten (siehe Beispiele).
Nun gibt es aber Variablen, die von Natur aus einen kontinuierlichen Wertebereich haben, z.B. wird man eine Entfernung vielleicht in Metern bestimmen wollen (mit beliebig vielen Nachkommastellen, also beliebig hoher Präzision). Für solche Variablen werden bedingte Dichten/Verteilungen vorgegeben, in denen kontinuierliche Elternknoten als Parameter dieser Funktionen auftauchen. Hat ein kontinuierlicher Knoten auch diskrete Eltern, so enthält er eine mehrdimensionale Tabelle (MDT) mit jeweils einer solchen bedingten Verteilung je Zustandskombination seiner diskreten Eltern (ungefähr so wie eine CPT für einen diskreten Knoten mit n Zuständen n Wahrscheinlichkeitswerte für jede Zustandskombination der Eltern enthält)1).
Der umgekehrte Fall, dass ein diskreter Knoten kontinuierliche Eltern hat, wird zumeist ausgeschlossen, wegen der Unmöglichkeit unendlich viele diskrete Verteilungen für die unendlich vielen Zustände kontinuierlicher Elternknoten zu definieren. Ansonsten gibt es apriori zwar keine Einschränkungen bezüglich der Struktur oder der Verteilungen, jedoch können einige Verfahren nur mit bestimmten Verteilungen umgehen - insbesondere sind hier linear abhängige Gauss-Verteilungen (kurz: "Conditional Gaussians") zu nennen. Dazu gleich mehr...
Nun gibt es aber Variablen, die von Natur aus einen kontinuierlichen Wertebereich haben, z.B. wird man eine Entfernung vielleicht in Metern bestimmen wollen (mit beliebig vielen Nachkommastellen, also beliebig hoher Präzision). Für solche Variablen werden bedingte Dichten/Verteilungen vorgegeben, in denen kontinuierliche Elternknoten als Parameter dieser Funktionen auftauchen. Hat ein kontinuierlicher Knoten auch diskrete Eltern, so enthält er eine mehrdimensionale Tabelle (MDT) mit jeweils einer solchen bedingten Verteilung je Zustandskombination seiner diskreten Eltern (ungefähr so wie eine CPT für einen diskreten Knoten mit n Zuständen n Wahrscheinlichkeitswerte für jede Zustandskombination der Eltern enthält)1).
Der umgekehrte Fall, dass ein diskreter Knoten kontinuierliche Eltern hat, wird zumeist ausgeschlossen, wegen der Unmöglichkeit unendlich viele diskrete Verteilungen für die unendlich vielen Zustände kontinuierlicher Elternknoten zu definieren. Ansonsten gibt es apriori zwar keine Einschränkungen bezüglich der Struktur oder der Verteilungen, jedoch können einige Verfahren nur mit bestimmten Verteilungen umgehen - insbesondere sind hier linear abhängige Gauss-Verteilungen (kurz: "Conditional Gaussians") zu nennen. Dazu gleich mehr...
Die einfachste Möglichkeit
mit kontinuierlichen Variablen umzugehen, ist eine Diskretisierung durchzuführen.
Dabei
wird der kontinuierliche Wertebereich in Intervalle
eingeteilt, die dann bestimmten Kategorien einer diskreten
Variable zugeordnet werden. So könnte man z.B. den
Bereich von 0m-1.60m der Kategorie "klein", 1.60m-1.85m der
Kategorie "mittel" und alles über 1.85m der Kategorie
"groß" zuordnen. Welche Kategorien sinnvoll sind,
hängt dabei natürlich stark vom konkreten
Anwendungsfall ab (so sind die genannten Kategorien zur
Einteilung vom Personen nach ihrer Körpergröße
vielleicht sinnvoll, während sie bei der Messung von
stellaren Entfernungen doch eher unbrauchbar sein
dürften).
Der Vorteil des Verfahrens besteht offensichtlich darin, dass man dann mit solchen diskretisierten Variablen ganz "normal" weiterarbeiten kann, d.h. alle Verfahren für diskrete Bayes'sche Netze zur Verfügung stehen. Ein Nachteil ist, dass man nur eine relativ geringe Auflösung bei der Diskretisierung wählen kann - denn mit mehr als einer Hand voll diskreten Zuständen wird man schnell in Komplexitätsprobleme laufen und zudem Probleme haben, die hohe Anzahl unabhängig wählbarer Parameter einzustellen. Will man die Parameter aus Daten lernen, braucht man eine entsprechend sehr große Datenmenge, um viele Parameter noch "sauber" schätzen zu können (grob gesagt müssen für jeden Parameter genügend Daten zur Schätzung zur Verfügung stehen. Als Faustformel kann man von ca. mind. 10 Beobachtungen pro Parameter ausgehen).
Der Vorteil des Verfahrens besteht offensichtlich darin, dass man dann mit solchen diskretisierten Variablen ganz "normal" weiterarbeiten kann, d.h. alle Verfahren für diskrete Bayes'sche Netze zur Verfügung stehen. Ein Nachteil ist, dass man nur eine relativ geringe Auflösung bei der Diskretisierung wählen kann - denn mit mehr als einer Hand voll diskreten Zuständen wird man schnell in Komplexitätsprobleme laufen und zudem Probleme haben, die hohe Anzahl unabhängig wählbarer Parameter einzustellen. Will man die Parameter aus Daten lernen, braucht man eine entsprechend sehr große Datenmenge, um viele Parameter noch "sauber" schätzen zu können (grob gesagt müssen für jeden Parameter genügend Daten zur Schätzung zur Verfügung stehen. Als Faustformel kann man von ca. mind. 10 Beobachtungen pro Parameter ausgehen).
Sampling-Verfahren
bieten einen Ansatz, Inferenz in kontinuierlichen und hybriden
Netzen zu betreiben.
LW-Sampling:
LW-Sampling lässt sich z.B. relativ einfach auf jede Art von Zusammenhängen übertragen und ist damit für kontinuierliche wie hybride Netze ohne eine prinzipielle Einschränkung auf bestimmte Verteilungsarten anwendbar. Es muss nur möglich sein, aus den Verteilungen "Samples" zu ziehen (das ist praktisch immer möglich). Aus der Gesamtzahl der Samples lässt sich dann für alle (unbeobachteten) Knoten eine A-Posteriori-Verteilung schätzen. Hier kann man sowohl parametrisierte Verfahren benutzen, bei denen versucht wird die Parameter einer vorgegebenen Verteilungsart zu schätzen (z.B. Mittelwert und Varianz bzw. Standardabweichung einer Normalverteilung), als auch nicht-parametrisierte Verfahren anwenden, wie z.B. einfach ein Histogramm ausgeben, was den Vorteil hat, dass die Art der Verteilung nicht vorher bekannt sein muss. Die folgenden Grafiken stellen eine solche Verteilung und mögliche Repräsentationen dar. Wobei die wahre Verteilung aus drei (unterschiedlich gewichteten) Normalverteilungen zusammengesetzt ist ("Mixture of Gaussians"), was z.B. bei hybriden Netzen mit diskreten Knoten und kontinuierlichen Knoten, die bedingte Gaussverteilungen verwenden ("CG-Knoten"), der Normalfall ist, während bei rein kontinuierlichen Netzen mit CG-Knoten nur einfache Normalverteilungen herauskommen können. Die Parameter einer solchen Mixture wären aber nur schwer zu schätzen. Eine einfache Normalverteilung kann die wahre Verteilung nur ungenügend abbilden, während ein Histogramm die tatsächliche Verteilung deutlich besser abzubilden vermag.
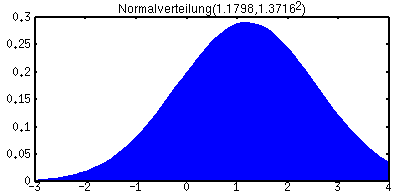
Eine aus 1000 Samples geschätzte einfache Nomalverteilung (keine Mixture) gibt die wahre Verteilung (s.o.) schlecht wieder (z.B. haben Werte um 1 hier die höchste Wahrscheinlichkeit, sind in Wahrheit aber recht unwahrscheinlich)
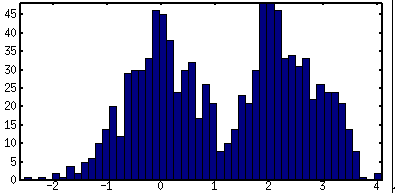
Aus denselben 1000 Samples gewonnenes Histogramm, welches die wahre Verteilung (s.o.) deutlich besser wiedergibt.
Gibbs-Sampling:
Nicht so ohne weiteres anwendbar ist dagegen Gibbs-Sampling, da hier ja aus den für jeden Knoten gegebenen bedingten Verteilungen für gegebene Elternzustände die bedingten Verteilungen gegeben alle Knoten des Markov-Blankets gebildet werden müssen, was in gewisser Weise dem Umdrehen von Kanten entspricht. Dafür muss aber die Bayes'sche Formel angewendet werden, was für beliebige Verteilungen nicht unbedingt möglich ist (schon garnicht effizient). Insbesondere stellen hybride Netze ein Problem dar, da dann ja auch Verteilungen diskreter Knoten für gegebene kontinuierliche Knoten ihres Markov-Blankets dargestellt werden müssten (also im Prinzip dasselbe Problem, wegen dem kontinuierliche Eltern diskreter Knoten verboten sind, s.o.). Möglich ist aber z.B. die Anwendung auf rein kontinuierliche Netze mit linear abhängigen Gaussverteilungen (Conditional Gaussians) da für diese die Exchange-Operation (die im nächsten Kapitel ausführlich dargestellt wird) benutzt werden kann, um die Verteilung über die Knoten des Markov-Blankets zu bilden.
LW-Sampling:
LW-Sampling lässt sich z.B. relativ einfach auf jede Art von Zusammenhängen übertragen und ist damit für kontinuierliche wie hybride Netze ohne eine prinzipielle Einschränkung auf bestimmte Verteilungsarten anwendbar. Es muss nur möglich sein, aus den Verteilungen "Samples" zu ziehen (das ist praktisch immer möglich). Aus der Gesamtzahl der Samples lässt sich dann für alle (unbeobachteten) Knoten eine A-Posteriori-Verteilung schätzen. Hier kann man sowohl parametrisierte Verfahren benutzen, bei denen versucht wird die Parameter einer vorgegebenen Verteilungsart zu schätzen (z.B. Mittelwert und Varianz bzw. Standardabweichung einer Normalverteilung), als auch nicht-parametrisierte Verfahren anwenden, wie z.B. einfach ein Histogramm ausgeben, was den Vorteil hat, dass die Art der Verteilung nicht vorher bekannt sein muss. Die folgenden Grafiken stellen eine solche Verteilung und mögliche Repräsentationen dar. Wobei die wahre Verteilung aus drei (unterschiedlich gewichteten) Normalverteilungen zusammengesetzt ist ("Mixture of Gaussians"), was z.B. bei hybriden Netzen mit diskreten Knoten und kontinuierlichen Knoten, die bedingte Gaussverteilungen verwenden ("CG-Knoten"), der Normalfall ist, während bei rein kontinuierlichen Netzen mit CG-Knoten nur einfache Normalverteilungen herauskommen können. Die Parameter einer solchen Mixture wären aber nur schwer zu schätzen. Eine einfache Normalverteilung kann die wahre Verteilung nur ungenügend abbilden, während ein Histogramm die tatsächliche Verteilung deutlich besser abzubilden vermag.

Eine aus 1000 Samples geschätzte einfache Nomalverteilung (keine Mixture) gibt die wahre Verteilung (s.o.) schlecht wieder (z.B. haben Werte um 1 hier die höchste Wahrscheinlichkeit, sind in Wahrheit aber recht unwahrscheinlich)

Aus denselben 1000 Samples gewonnenes Histogramm, welches die wahre Verteilung (s.o.) deutlich besser wiedergibt.
Gibbs-Sampling:
Nicht so ohne weiteres anwendbar ist dagegen Gibbs-Sampling, da hier ja aus den für jeden Knoten gegebenen bedingten Verteilungen für gegebene Elternzustände die bedingten Verteilungen gegeben alle Knoten des Markov-Blankets gebildet werden müssen, was in gewisser Weise dem Umdrehen von Kanten entspricht. Dafür muss aber die Bayes'sche Formel angewendet werden, was für beliebige Verteilungen nicht unbedingt möglich ist (schon garnicht effizient). Insbesondere stellen hybride Netze ein Problem dar, da dann ja auch Verteilungen diskreter Knoten für gegebene kontinuierliche Knoten ihres Markov-Blankets dargestellt werden müssten (also im Prinzip dasselbe Problem, wegen dem kontinuierliche Eltern diskreter Knoten verboten sind, s.o.). Möglich ist aber z.B. die Anwendung auf rein kontinuierliche Netze mit linear abhängigen Gaussverteilungen (Conditional Gaussians) da für diese die Exchange-Operation (die im nächsten Kapitel ausführlich dargestellt wird) benutzt werden kann, um die Verteilung über die Knoten des Markov-Blankets zu bilden.
Linear abhängige bedingte
Gauss-Verteilungen (auch Conditional-Gaussians - oder ganz
kurz CGs) haben, wie bereits angedeutet, eine besondere
Bedeutung, da einige Verfahren nur solche Verteilungen
erlauben (oder solche auf denen dieselben Operationen
definiert werden können). Daher werden CGs in diesem
Abschnitt genauer beschrieben.
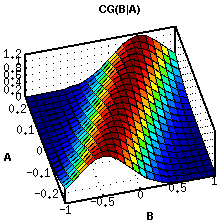
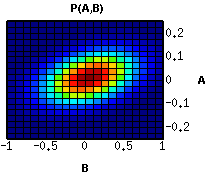
Links: Conditional Gaussian CG(B|A): Für jeden Wert von A gibt es eine Normalverteilung über B, deren Mittelwert von A abhängt.
Rechts: Ist auch A normalverteilt ergibt sich eine Gesamtverteilung über A und B, die etwa dieses Aussehen hat
Um einen kontinuierlichen Knoten X in einem (potenziell) hybriden Bayes'schen Netz zu beschreiben, wird für diesen Knoten X für jede Zustandskombination der diskreten Elternknoten eine CG in einer entsprechenden multidimensionalen Tabelle (MDTCG) (ähnlich einer CPT) abgelegt. Wobei jede dieser CGs ihrerseits von den kontinuierlichen Elternknoten linear abhängt, d.h. es wird ein Faktor für jeden dieser Elternknoten, sowie ein konstanter Offset definiert. Eine einzelne CG ist dabei wie folgt definiert:
Dies ist im Prinzip eine Anwendung der Bayes'schen Formel.
Eine "Set-Head-Operation" könnte man auch definieren, diese würde aber einfach eine unbedingte CG (also eine einfache Normalverteilung) erzeugen, die den zu setzenden Wert als mean und die Varianz var=0 hätte.
Um zwei Multidimensionale Tafeln von CGs (MDTCG) miteinander verrechnen zu können (insbesondere wenn man die Exchange-Operation auf allen enthaltenen CGs anwenden will) ist es nötig die kleinere der beiden auf die Größe der anderen "aufzublasen". Diese Operation nenne ich hier die "Reshape-Operation". Dazu wird jede CG entsprechend oft in die MDTCG-Elemente der zuvor nicht enthaltenen Dimensionen kopiert. Ein Beispiel sollte reichen um klar zu machen was die Reshape-Operation bewirken soll:
Hierbei wird die Ausgangs- in eine MDTCG umgeformt, die zusätzlich zur Dimension des diskreten Knotens A (mit den beiden Zuständen a1 und a2), noch die Dimension des diskreten Knotens B (mit den beiden Zuständen b1 und b2) enthält - das ist wieder equivalent zu dem was man mit zwei multidemsionalen Wahrscheinlichkeitstafeln (z.B. CPTs) machen muss, wenn man diese z.B. multiplizieren will.1)
Nicht-Lineare Zusammenhänge:
Mit Conditional Gaussians lassen sich nur lineare Abhängigkeiten zwischen Variablen darstellen. Eine Möglichkeit auch nicht lineare Abhängigkeiten abzubilden bestünde natürlich prinzipiell darin, Verteilungen zu benutzen, die auch nicht lineare Abhängigkeiten unterstützen. Dies hört sich trivial an, ist aber leider nicht so ohne Weiteres möglich. Eine einfachere Möglichkeit besteht darin statt der Original-Variablen, z.B. A, B, C transformierte Variablen AT, BT, CT zu verwenden, wobei aT = fa(a), bT = fb(b), cT = fc(c). Im Bayes'schen Netz sind dann statt der Original- die transformierten Variablen durch Knoten repräsentiert. Um die Ergebnisse auch wieder eindeutig zurück in den Werte-Bereich der Original-Variablen transformieren zu können, wird eine - zumindest im interessierenden Bereich - bijektive Transformation benötigt, was die Möglichkeiten natürlich deutlich einschränkt. Es wird also z.B. Funktionen benötigt, so dass a = ga(aT), b = gb(bT), c = gc(cT). Noch störender ist, aber, dass man ja mit dieser Methode, die Variable als solche und nicht einzelne Abhängigkeiten verändert. Hat man z.B. zwei Variablen B und C, die beide von einer Variablen A abhängen, die eine jedoch einen linearen, die andere dagegen einen nicht-linearen Zusammenhang mit A aufweist, so gibt es offenkundig keine Transformation für A, die beide Fälle abdecken kann. Versucht man es über unterschiedliche Transformationen von B und C abzubilden, sind davon u.U. wieder weitere Knoten und deren Abhängigkeiten zu den originalen Variablen B und C betroffen. Ein weiteres Problem besteht darin, dass durch eine solche Transformation auch die Verteilungskurven ungleichmäßig verzerrt werden, so dass sie - bezogen auf die Original-Variable - einerseits keine Normalverteilung mehr repräsentieren; andererseits aber die Verteilungsart auch nicht frei wählbar ist, da sie durch die darzustellende Abhängigkeit zwischen den Variablen getrieben ist und immer eine irgendwie verzerrte Normalverteilung dabei herauskommen wird.
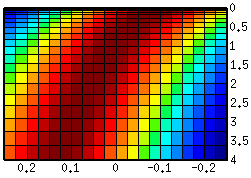
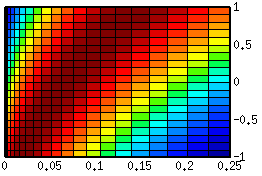
Links: CG(B|AT) mit nicht linear (rück-)transformierter Tail-Variable A (Y-Achse). Verteilungen über B, gegeben einen konkreten Wert für A bzw AT, bleiben hier unverzerrte Normalverteilungen, dafür wäre die Verteilung von A verzerrt (hier nicht dargestellt).
Rechts: CG(BT|A) mit nicht linear (rück-)transformierter Head-Variable B (X-Achse). Verteilungen über B, gegeben einen konkreten Wert für A bzw. AT, sind keine Normalverteilung mehr, sondern verzerrt worden (die linke Flanke ist jeweils steiler als die rechte).


.
Links: Conditional Gaussian CG(B|A): Für jeden Wert von A gibt es eine Normalverteilung über B, deren Mittelwert von A abhängt.
Rechts: Ist auch A normalverteilt ergibt sich eine Gesamtverteilung über A und B, die etwa dieses Aussehen hat
Um einen kontinuierlichen Knoten X in einem (potenziell) hybriden Bayes'schen Netz zu beschreiben, wird für diesen Knoten X für jede Zustandskombination der diskreten Elternknoten eine CG in einer entsprechenden multidimensionalen Tabelle (MDTCG) (ähnlich einer CPT) abgelegt. Wobei jede dieser CGs ihrerseits von den kontinuierlichen Elternknoten linear abhängt, d.h. es wird ein Faktor für jeden dieser Elternknoten, sowie ein konstanter Offset definiert. Eine einzelne CG ist dabei wie folgt definiert:
CG(X|Y1...Yn) = Gauss(meanx + fx|y1 × y1 + ... + fx|yn × yn, varx) oder Gauss(fx|y0 × y0 + fx|y1 × y1 + ... + fx|yn × yn, varx)
wobei:
- Y1...Yn die kontinuierlichen Elternknoten von X sind, deren konkrete Werte mit y1...yn bezeichnet werden,
- y0 in der zweiten Schreibweise immer = 1 ist,
- fx1...fxn die linearen Abhängigkeitsfaktoren für diese Werte der Elternknoten sind,
- mean (bzw. fx|y0 in der zweiten Schreibweise) der Mittelwert der Gaussverteilung ist (wenn alle Eltern den Wert 0 haben, oder es keine Eltern gibt und aus der CG damit eine einfache Normalverteilung wird),
- var die Varianz (quadrierte Standardabweichung) der Gaussverteilung ist und
- X in einer CG auch als Head-Variable und die Y1...Yn auch als Tail-Variablen bezeichnet werden.
Für einige Ansätze
ist es notwendig, dass die Exchange-Operation
(effizient) durchgeführt werden kann. Mit der
Exchange-Operation werden zwei CGs in zwei andere CGs
überführt, wie in folgender Tabelle dargestellt
ist:
| original |
exchanged |
|
| exchange |
CG(Z|Y,V1...Vn) | CG(Z|V1...Vn) |
| CG(Y|V1...Vn) | CG(Y|Z,V1...Vn) |
Dies ist im Prinzip eine Anwendung der Bayes'schen Formel.
Der folgende Kasten
erklärt die Exchange-Operation im Detail und kann auch
übersprungen werden...
Die
Exchange-Operation auf Conditional Gaussians im Detail
Hier nochmal die Ausgangs- und Ziel-CGs vor und nach der Anwendung der Exchange-Operation:
Die Parameter (Faktoren, Mean-Werte und Varianzen) der sich ergebenden CGs werden folgendermaßen berechnet:
Dabei sind der Einfachheit halber fx|vo := meanx und v0 := 1 gesetzt worden (d.h. die zweite oben dargestellte Schreibweise wurde benutzt). Außerdem wird für jeden Faktor für Knoten, die nur in einer der beiden originalen CGs auftauchen in der anderen der Wert 0 angenommen (ebenso in allen folgenden Gleichungen).
für CG(Y|Z,V1...Vn) müssen drei Fälle unterschieden werden:
Hier nochmal die Ausgangs- und Ziel-CGs vor und nach der Anwendung der Exchange-Operation:
| original |
exchanged |
|
| exchange |
CG(Z|Y,V1...Vn) | CG(Z|V1...Vn) |
| CG(Y|V1...Vn) | CG(Y|Z,V1...Vn) |
Die Parameter (Faktoren, Mean-Werte und Varianzen) der sich ergebenden CGs werden folgendermaßen berechnet:
für CG(Z|V1...Vn):
| ( |
|
) |
||||
| CG(Z|V1...Vn) | =
|
|
|
(fz|vi
+ fz|y × fy|vi)
× vi
, varz + fz|y2
× vary |
||
|
|
Dabei sind der Einfachheit halber fx|vo := meanx und v0 := 1 gesetzt worden (d.h. die zweite oben dargestellte Schreibweise wurde benutzt). Außerdem wird für jeden Faktor für Knoten, die nur in einer der beiden originalen CGs auftauchen in der anderen der Wert 0 angenommen (ebenso in allen folgenden Gleichungen).
für CG(Y|Z,V1...Vn) müssen drei Fälle unterschieden werden:
- vary > 0 und
varz > 0:
CG(Y|Z,V1...Vn)
=
Gauss ( 
i=0
(fy|vi × varz - fz|vi × fz|y × vary) × vi
, varz × vary ) varz + fz|y2 × vary varz + fz|y2 × vary
- vary > 0 (und
varz = 0):
CG(Y|Z,V1...Vn)
=
Gauss (
z -
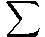
i=0 fz|vi × vi , 0 )
fz|y
- sonst (vary = 0 und varz >= 0):
(
n
)
CG(Y|Z,V1...Vn) =
Gauss 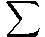
fy|vi × vi , 0
i = 0
Ebenfalls teilweise
notwendig, aber viel weniger restriktiv ist die Anforderung,
dass es eine Set-Tail-Operation
geben muss, mit deren Hilfe eine CG so modifiziert wird,
dass für eine Tail-Variable ein fester (beobachteter)
Wert gesetzt werden kann, wodurch die Tail-Variable aus der
CG entfernt werden kann.
| set |
original |
nach Set-Teil |
| Vi=v | CG(Z|V1...Vi...Vn) | CG*(Z|V1...Vi-1,Vi+1...Vn) |
Die
Set-Tail-Operation auf Conditional Gaussians im Detail
Auch hier nochmal, der Vollständigkeit halber, die CGs bevor und nachdem der Wert v für Vi gesetzt wurde:
Die Parameter (Faktoren, Mean-Werte und Varianzen) der sich ergebenden CG*(Z|V1...Vi-1,Vi+1...Vn) werden folgendermaßen berechnet:
wobei:
Auch hier nochmal, der Vollständigkeit halber, die CGs bevor und nachdem der Wert v für Vi gesetzt wurde:
| set |
original |
nach Set-Teil |
| Vi=v | CG(Z|V1...Vi...Vn) | CG*(Z|V1...Vi-1,Vi+1...Vn) |
Die Parameter (Faktoren, Mean-Werte und Varianzen) der sich ergebenden CG*(Z|V1...Vi-1,Vi+1...Vn) werden folgendermaßen berechnet:
| CG*(Z|V1...Vi-1,Vi+1...Vn) | =
|
|
( | fz|v1 × v1 + ... + fz|vi-1 × vi-1 + fz|vi+1 × vi+1 + ... + fz|vn × vn + meanz* ,
varz |
) |
wobei:
meanz* = meanz
+ fz|vi × v
Eine "Set-Head-Operation" könnte man auch definieren, diese würde aber einfach eine unbedingte CG (also eine einfache Normalverteilung) erzeugen, die den zu setzenden Wert als mean und die Varianz var=0 hätte.
Um zwei Multidimensionale Tafeln von CGs (MDTCG) miteinander verrechnen zu können (insbesondere wenn man die Exchange-Operation auf allen enthaltenen CGs anwenden will) ist es nötig die kleinere der beiden auf die Größe der anderen "aufzublasen". Diese Operation nenne ich hier die "Reshape-Operation". Dazu wird jede CG entsprechend oft in die MDTCG-Elemente der zuvor nicht enthaltenen Dimensionen kopiert. Ein Beispiel sollte reichen um klar zu machen was die Reshape-Operation bewirken soll:
|
wird z.B. zu |
|
|||||||||||||||||||
Hierbei wird die Ausgangs- in eine MDTCG umgeformt, die zusätzlich zur Dimension des diskreten Knotens A (mit den beiden Zuständen a1 und a2), noch die Dimension des diskreten Knotens B (mit den beiden Zuständen b1 und b2) enthält - das ist wieder equivalent zu dem was man mit zwei multidemsionalen Wahrscheinlichkeitstafeln (z.B. CPTs) machen muss, wenn man diese z.B. multiplizieren will.1)
Nicht-Lineare Zusammenhänge:
Mit Conditional Gaussians lassen sich nur lineare Abhängigkeiten zwischen Variablen darstellen. Eine Möglichkeit auch nicht lineare Abhängigkeiten abzubilden bestünde natürlich prinzipiell darin, Verteilungen zu benutzen, die auch nicht lineare Abhängigkeiten unterstützen. Dies hört sich trivial an, ist aber leider nicht so ohne Weiteres möglich. Eine einfachere Möglichkeit besteht darin statt der Original-Variablen, z.B. A, B, C transformierte Variablen AT, BT, CT zu verwenden, wobei aT = fa(a), bT = fb(b), cT = fc(c). Im Bayes'schen Netz sind dann statt der Original- die transformierten Variablen durch Knoten repräsentiert. Um die Ergebnisse auch wieder eindeutig zurück in den Werte-Bereich der Original-Variablen transformieren zu können, wird eine - zumindest im interessierenden Bereich - bijektive Transformation benötigt, was die Möglichkeiten natürlich deutlich einschränkt. Es wird also z.B. Funktionen benötigt, so dass a = ga(aT), b = gb(bT), c = gc(cT). Noch störender ist, aber, dass man ja mit dieser Methode, die Variable als solche und nicht einzelne Abhängigkeiten verändert. Hat man z.B. zwei Variablen B und C, die beide von einer Variablen A abhängen, die eine jedoch einen linearen, die andere dagegen einen nicht-linearen Zusammenhang mit A aufweist, so gibt es offenkundig keine Transformation für A, die beide Fälle abdecken kann. Versucht man es über unterschiedliche Transformationen von B und C abzubilden, sind davon u.U. wieder weitere Knoten und deren Abhängigkeiten zu den originalen Variablen B und C betroffen. Ein weiteres Problem besteht darin, dass durch eine solche Transformation auch die Verteilungskurven ungleichmäßig verzerrt werden, so dass sie - bezogen auf die Original-Variable - einerseits keine Normalverteilung mehr repräsentieren; andererseits aber die Verteilungsart auch nicht frei wählbar ist, da sie durch die darzustellende Abhängigkeit zwischen den Variablen getrieben ist und immer eine irgendwie verzerrte Normalverteilung dabei herauskommen wird.


.
Links: CG(B|AT) mit nicht linear (rück-)transformierter Tail-Variable A (Y-Achse). Verteilungen über B, gegeben einen konkreten Wert für A bzw AT, bleiben hier unverzerrte Normalverteilungen, dafür wäre die Verteilung von A verzerrt (hier nicht dargestellt).
Rechts: CG(BT|A) mit nicht linear (rück-)transformierter Head-Variable B (X-Achse). Verteilungen über B, gegeben einen konkreten Wert für A bzw. AT, sind keine Normalverteilung mehr, sondern verzerrt worden (die linke Flanke ist jeweils steiler als die rechte).
| 1) | wobei implementierungsseitig darauf geachtet
werden muss dass die Instanzen der beiden CGs
tatsächlich kopiert werden, auch wenn diese
zunächst noch dieselben CGs darstellen |
Da Sampling-Verfahren
natürlich auch bei kontinuierlichen Verteilungen
prinzipielle Probleme haben (Ungenauigkeiten bis hin zum
völligen Versagen auf bestimmten Verteilungen mit
bestimmten Evidenzen) sind auch exakte Verfahren entwickelt
worden. Eines davon ist das von Cowell [1] beschriebene Verfahren,
das hier im Folgenden vorgestellt wird. Dieses, wie andere
exakte Verfahren auch, schränkt kontinuierliche Knoten
auf solche mit bedingten linearen
Gauss-Verteilungen ein (bzw. solchen für die in
gleicher Weise die sogenannte "Exchange"-Operation
definiert werden kann, s.o.)
Strong-(Semi-)Elimination-Tree:
Der Algorithmus von Cowell basiert auf einem sogenannten Strong-(Semi-)Elimination-Tree.
Ein Elimination-Tree
ist im Prinzip ein Junction-Tree,
bei dem aber zu jedem eliminierten Knoten eine Clique gebildet wird, d.h.
auch dann, wenn diese Clique Teilmenge einer anderen Clique
ist (siehe auch den Beispiel-Elimination-Tree
im folgenden Abschnitt). Um den
Unterschied zu verdeutlichen, werden diese "Cliquen" eines
Elimination-Trees im Weiteren "Cluster" genannt.Für den Algorithmus unabdingbar ist - anders als bei normalen Junction-Trees - dass die Cluster in einer ganz bestimmten Art und Weise zu einem Tree verbunden werden und nicht einfach nur in irgendeiner, die Running-Intersection-Eigenschaft gewährleistenden Form.
Algorithmus
zum Verbinden der Cluster zu einem Elimination-Tree
Über alle Cluster Ci aus der Menge aller Cluster C in der umgekehrten Reihenfolge ihrer Erzeugung (umgekehrte Eliminierungs-Reihenfolge), die mehr als einen Knoten enthalten:
Über alle Cluster Ci aus der Menge aller Cluster C in der umgekehrten Reihenfolge ihrer Erzeugung (umgekehrte Eliminierungs-Reihenfolge), die mehr als einen Knoten enthalten:
- Finde den in Knoten Xj aus Ci, der in der Eliminierungsreihenfolge am weitesten vorne steht (also der früheste eliminierte Knoten), wobei Xj nicht der Knoten Xi sein darf, durch dessen Eliminierung das Cluster Ci gebildet wurde (daher müssen auch nur Cluster mit mehr als einem Knoten geprüft werden, weil sonst kein anderer Knoten enthalten ist)
- Verbinde das Cluster Cj, das durch die Eliminierung des Knotens Xj entstanden ist, mit dem Cluster Ci.
Handelt es sich um ein rein diskretes Netz,
kann man mit einem Elimination-Tree genauso rechnen wie mit
einem Junction-Tree. Dies ist nur ineffizienter, weil noch
Cluster enthalten sind, die Teilmenge anderer Cluster sind.
Dies kann durch eine "Aggregation" dieser Cluster aber
behoben und der Elimination-Tree dadurch in einen echten
Junction-Tree überführt werden (dazu gleich mehr).
Für den Algorithmus von Cowell ist es weiterhin nötig, dass zunächst alle kontinuierlichen Knoten eliminiert werden, bevor der erste diskrete Knoten eliminiert werden darf. Abgesehen von dieser Restriktion können die üblichen Optimierungsverfahren eingesetzt werden. Allerdings sind der Optimierung dadurch für bestimmte Netzstrukturen dann doch enge Grenzen gesetzt. Es gilt:
Für den Algorithmus von Cowell ist es weiterhin nötig, dass zunächst alle kontinuierlichen Knoten eliminiert werden, bevor der erste diskrete Knoten eliminiert werden darf. Abgesehen von dieser Restriktion können die üblichen Optimierungsverfahren eingesetzt werden. Allerdings sind der Optimierung dadurch für bestimmte Netzstrukturen dann doch enge Grenzen gesetzt. Es gilt:
Zwei
diskrete Knoten A
und B, die
kontinuierliche Kind-Knoten X und Y
haben, werden in mindestens einem Cluster gemeinsam
enthalten sein, wenn X
und Y über
mindestens einen Pfad verbunden sind, der nur über
kontinuierliche Knoten verläuft (das gilt insbesondere
auch dann, wenn X
und Y direkt
verbunden sind, oder X
und Y derselbe
Knoten ist).
Es können also u.U. "unnötig" große Cluster mit diskreten Knoten entstehen, die ohne die o.g. Restriktion der Eliminierungsreihenfolge nie aufgetreten wären.
Auf diese Art ist aber sichergestellt, dass (für zusammenhängende Graphen) ein rein diskreter Teil des Junction-Trees entsteht, d.h. zu jedem diskrete Knoten gibt es ein rein diskretes Home-Cluster (entsprechend einer Home-Clique) und für je zwei rein diskrete Cluster gibt es einen Pfad der sie verbindet, der selbst auch nur über rein diskrete Cluster verläuft. Wichtiger für den Algorithmus ist aber, dass es zu jedem hybriden Cluster Ch in Richtung des Strong-Root-Clusters, einen diskreten "Boundary-Cluster" Cb gibt, der auf jeden Fall alle relevanten diskreten Knoten enthält, von dem die kontinuierlichen Knoten des Clusters Ch abhängig sein können.
Schneidet man alle nicht rein diskreten Cluster von einem solchen Elimination-Tree ab, hat man einen gültigen Elimination-Tree für den rein diskreten Teil des Netzes. Legt man nun als Root-Knoten (der hier "strong Root" genannt wird) einen der rein diskreten Cluster fest, kann man im rein diskreten Teil des dann sogenannten "Strong-Elimination-Trees" genauso rechnen wie in einem normalen Junction-Tree. Man kann diesen Teil (und nur diesen) auch in einen "echten" Junction-Tree überführen, indem die Cluster, die Teilmengen anderer Cluster sind, aggregiert werden. Die gesamte Struktur wird danach "Strong-Semi-Elimination-Tree" genannt, weil nur noch der nicht rein diskrete Teil ein "echter" Elimination-Tree ist, während der andere in einen Junction-Tree überführt wurde.
Der Aggregations-Algorithmus
für (hybride) Elimination-Trees
- Erzeuge eine Liste L aller Cluster in der Reihenfolge ihrer Entstehung (enstprechend der Eliminierungsreihenfolge)
- Erzeuge eine zweite List J
die nach Abschluss die neue Liste L
aller Cluster wird (diese ist nicht mehr unbedingt
in der Eliminierungsreihenfolge und wird hier auch
nicht weiter benötigt, da sowieso nur rein
diskrete Cluster aggregiert werden können)
- Solange L nicht leer ist:
- Entferne das letzte Cluster Ci
aus L
- Wenn Ci rein diskret ist (nur diskrete Knoten enthält) und Teilmenge mind. eines rein diskreten Kind-Clusters von Ci ist:
- Finde das Kind-Cluster Cj von
Ci,
welches (gem. Eliminierungsreihenfolge) zuletzt
erzeugt wurde wobei nur Cluster
betrachtet werden, die rein diskret sind und
die alle Knoten von Ci enthalten1)
- Entferne Ci aus dem Elimination-Tree und setze stattdessen Cj ein (dh. alle bisherigen Eltern von Ci = pa(Ci) werden zu Eltern von Cj gemacht und alle bisherigen Kinder von Ci = ch(Cj) außer Cj selbst werden zu Kindern von Cj gemacht)
- Setze Cj an das Ende der Liste L
(d.h. es wird an der Ursprünglichen
Position entfernt), so dass dieses das
nächste Cluster Ci wird.
- andernfalls setze Ci an den Ende von J
Hat man es dagegen weder mit
einem rein diskreten, noch mit einem hybriden Netz, sondern
mit einem rein kontinuierlichen Netz zu tun, dann sind der
Optimierung der Eliminierunsgreihenfolge keine Grenzen
gesetzt und als ("strong") Root-Cluster kann und muss ein
(rein) kontinuierlicher Cluster genommen werden (denn es
gibt ja keine anderen).
Initialisierung des Strong-(Semi-)Elimination-Trees:
Die rein diskreten Cluster werden wie bei normalen Junction-Trees initialisiert (die CPT jedes diskreten Knotens wird in die Wahrscheinlichkeitstafel einer rein diskreten Home-Clique / eines Home-Clusters einmultipliziert, welche zuvor mit 1en initialisiert wurde; die Separatorentafeln zwischen rein diskreten Clustern werden ebenfalls mit 1en initialisiert).
Für jeden kontinuierlichen Knoten Xi wird nun ebenfalls ein Home-Cluster gesucht. Die multidimensionale Tafel (MDTCG), die für jede Zustandskombination der diskreten Elternknoten von Xi eine Conditional Gaussian (CG) enthält, die wiederum von den kontinuierlichen Eltern abhängig ist, wird in diesem Home-Cluster abgelegt - und zwar entweder:
Initialisierung des Strong-(Semi-)Elimination-Trees:
Die rein diskreten Cluster werden wie bei normalen Junction-Trees initialisiert (die CPT jedes diskreten Knotens wird in die Wahrscheinlichkeitstafel einer rein diskreten Home-Clique / eines Home-Clusters einmultipliziert, welche zuvor mit 1en initialisiert wurde; die Separatorentafeln zwischen rein diskreten Clustern werden ebenfalls mit 1en initialisiert).
Für jeden kontinuierlichen Knoten Xi wird nun ebenfalls ein Home-Cluster gesucht. Die multidimensionale Tafel (MDTCG), die für jede Zustandskombination der diskreten Elternknoten von Xi eine Conditional Gaussian (CG) enthält, die wiederum von den kontinuierlichen Eltern abhängig ist, wird in diesem Home-Cluster abgelegt - und zwar entweder:
- im sogenannten LP-Potenzial des Home-Clusters, wenn der Xi der Knoten ist durch dessen Eliminierung das Cluster entstand2), oder
- sie wird einer Liste von Postbags hinzugefügt, wenn das nicht der Fall ist (in den Postbags können also mehrere MDTCG abgelegt werden3).
Die Separatoren zwischen
hybriden Clustern und diskreten und hybriden Clustern sind
reine Kanten ohne interne Datenstrukturen, wie sie für
die "normalen" Separatoren im diskreten Teil benötigt
werden (Diese Beschreibung weicht etwas von der in [1] verwendeten
ab).
Als nächstes müssen die Potenziale, die noch in den Postbags abgelegt sind, so umgeformt und verteilt werden, dass die Postbags hinterher leer sind und jedes Cluster Ci ein zu seinem Eliminierungsknoten Xi passendes LP-Potenzial enthält. Diese Phase bezeichne ich hier als "Collecting Postbags".
Als nächstes müssen die Potenziale, die noch in den Postbags abgelegt sind, so umgeformt und verteilt werden, dass die Postbags hinterher leer sind und jedes Cluster Ci ein zu seinem Eliminierungsknoten Xi passendes LP-Potenzial enthält. Diese Phase bezeichne ich hier als "Collecting Postbags".
Collecting Postbags
- Iteriere in der Entstehungsreihenfolge
(Eliminierungsreihenfolge) über alle nicht rein
diskreten Cluster Ci4)
- Nun werden die Postbags in Richtung zur
Root-Clique weiterverteilt, wobei u.U.
Exchange-Operationen auf den Postbags
durchgeführt werden. Dieser Vorgang
entspricht einem Umdrehen von Kanten im
ursprünglichen Bayes'schen Netz. Damit dabei
keine gerichteten Zyklen entstehen, muss eine
bestimmte Reihenfolge eingehalten werden. Ohne die
Details hier darzustellen, ist das die
"topologische Reihenfolge" der Knoten im
originalen Bayes-Netz5).
Daher werden die MDTCG
im Postbag anhand der topologischen Reihenfolge
der Head-Variablen der enthaltenen CGs5)
sortiert und in dieser Reihenfolge verarbeitet.
- Solange die Liste der Postbags nicht leer ist:
- Entferne die erste MDTCG aus der Liste der Postbags
- Wenn der Eliminierungsknoten Xi in den Tail-Variablen der CGs des aktuellen MDTs vorkommt:
- Erweitere die aktuelle Postbag-MDTCG
um die Dimensionen (diskreter Knoten) des MDTCG
des LP-Potenzials des aktuellen Clusters Ci,
indem die CGs für noch nicht vorhandene
Dimensionen entsprechend kopiert werden
(praktisch genauso wie unter 1)
beschrieben).
- Führe die Exchange-Operation auf allen CGs der aktuellen Postbag-MDTCG und den entsprechenden CGs im LP-Potenzial-MDTCG des Clusters Ci aus.
- Die aktuelle Postbag-MDTCG
wird nun an das Parent-Cluster Cj
(also in Richtung zum Strong-Root-Cluster)
weitergereicht7).
Anschließend hat jedes
Cluster Ci ein LP-Potenzial,
welches aus einer MDTCG besteht,
deren CGs den Eliminierungsknoten des Clusters Xi als Head-Variable
haben. Zudem sind die Postbag-Listen aller Cluster nun leer
(diese werden zwar noch weiter benutzt, werden dabei aber
nie wieder mehr als ein MDTCG
gleichzeitig enthalten).
Einbringen von Evidenz (Beobachtungen) in den Strong-(Semi-)Elimination-Tree:
Nachdem der Strong-(Semi-)Elimination-Tree initialisiert wurde, kann Evidenz eingebracht werden. Für diskrete Knoten passiert das wie für rein diskrete Junction-Trees, indem der Finding-Vektor in die Wahrscheinlichkeitstafel eines (rein diskreten) Clusters einmultipliziert wird. Für kontinuierliche Knoten ist der Ablauf komplizierter, da die Evidenz u.U. zunächst in mehrere Cluster gesetzt werden muss und die CG-Verteilungen im Cluster, welches zu dem beobachteten Knoten gehört, in Richtung einer diskreten "Boundary-Clique" weitergegeben werden und dabei zu (unbedingten) Normalverteilungen umgeformt werden müssen, um schließlich eine Gewichtstabelle an dieses Boundary-Cluster übergeben zu können. Der folgende Kasten beschreibt den Ablauf im Detail:
Einbringen von Evidenz (Beobachtungen) in den Strong-(Semi-)Elimination-Tree:
Nachdem der Strong-(Semi-)Elimination-Tree initialisiert wurde, kann Evidenz eingebracht werden. Für diskrete Knoten passiert das wie für rein diskrete Junction-Trees, indem der Finding-Vektor in die Wahrscheinlichkeitstafel eines (rein diskreten) Clusters einmultipliziert wird. Für kontinuierliche Knoten ist der Ablauf komplizierter, da die Evidenz u.U. zunächst in mehrere Cluster gesetzt werden muss und die CG-Verteilungen im Cluster, welches zu dem beobachteten Knoten gehört, in Richtung einer diskreten "Boundary-Clique" weitergegeben werden und dabei zu (unbedingten) Normalverteilungen umgeformt werden müssen, um schließlich eine Gewichtstabelle an dieses Boundary-Cluster übergeben zu können. Der folgende Kasten beschreibt den Ablauf im Detail:
Setzen von kontinuierlicher
Evidenz
- Für einen kontinuierliche Knoten Xi
wird der beobachtete Wert xi8)
in alle CGs aller LP-Potenziale aller Cluster
eingebracht, die diesen Knoten als Tail-Variable
enthalten. Das können nur solche Cluster sein,
die vor der Eliminierung von Xi
entstanden sind. Dazu werden diese CGs mit der Set-Tail-Operation
und dem beobachteten Wert xi modifiziert.
- Für das Cluster Ci welches mit der Eliminierung von Xi selbst entstanden ist wird eine Kopie seines LP-Potenzials in den Postbag abgelegt.
- Nun wird eine Push-Operation
durchgeführt, mit der diese Kopie in Richtung
Root-Cluster weitergereicht wird, bis ein rein
diskretes Cluster (Boundary-Cluster) erreicht wird:
- Dazu wird zunächst das aktuelle Cluster Ca gleich dem Ausgangscluster Ci gesetzt.
- Wenn es ein hybrides Elterncluster Cp von Ca gibt, dann lege eine (an die Größe der LP-Potenzial-MDTCG's von Cp angepasste) Kopie des Postbag-MDTCG's von Ca in den Postbag von Cp.
- Wenn Cp noch "aktiv" ist, d.h. wenn es noch keine zuvor eingebrachte Evidenz für den Eliminierungsknoten Xp von Cp gab:
- Führe die Exchange-Operation auf allen CGs des LP-Potenzials mit allen entsprechenden CGs des Postbags von Cp aus
- Modifiziere alle CGs des LP-Potenzials von Cp mit der Set-Tail-Operation und dem beobachteten Wert von Xi.
- Der Postbag von Ca kann nun wieder geleert werden.
- Setze Ca := Cp und fahre fort bis ein Boundary-Cluster erreicht wird
- Ist ein diskretes Boundary Cluster Cp
erreicht worden9),
so enthält das Postbag-MDTCG
von Ca
nur noch "unbedingte" CGs (also solche ohne
Tail-Variablen) mit Xi als Head-Variable.
Das entspricht einer normalen Gauss- oder
Normalverteilung über Xi. Aus diesen
Normalverteilungen wird nun eine multidimensionale
Gewichtstabelle berechnet, die für jede CG im
Postbag-MDTCG einen
Gewichtwert enthält, der sich aus dem
Funktionswert der jeweiligen CG für x = xi
ergibt. Diese Gewichttabelle wird dann (ähnlich
wie diskrete Evidenz) in die
Wahrscheinlichkeitstabelle des Boundary-Clusters
einmultipliziert.
Propagation im Strong-(Semi-)Elimination-Tree:
Es wird nur im diskreten
Teil propagiert. Dazu kann prinzipiell jedes Verfahren
für Junction-Trees verwendet werden.
Berechnen der A-Posteriori-Verteilungen:
Für einen diskrete Knoten Xd passiert die Berechnung der resultierenden A-Posteriori-Verteilungen wie in normalen, rein diskreten Junction-Trees, indem die Verteilung aus irgendeinem Cluster, welches den betreffenden Knoten enthält, durch Marginalisierung gewonnen wird (z.B. dem Home-Cluster).
Für kontinuierliche Knoten ist der Ablauf auch hier wesentlich komplexer, da erneut die MDTCG des LP-Potenzials des Eliminierungs-Clusters Ci des betreffenden Knotens Xi, zunächst wieder in Richtung eines Boundary-Clusters (mittels einer zweiten Push-Operation) weitergeleitet und dabei über die Exchange-Operation modifiziert werden muss, um schließlich aus dem Boundary-Cluster heraus mit einer Gewichtung versehen zu werden. Am Ende kommt also i.d.R. keine einzelne Normalverteilung heraus (außer bei rein kontinuierlichen Netzen), sondern eine "Mixture of Gaussians" in der mehrere Normalverteilungen mit Gewichten versehen wurden. Die folgende Grafik stellt eine solche Verteilung dar (das im Abschnitt über Sampling gezeigte Histogramm stellt übrigens dieselbe Verteilung dar).
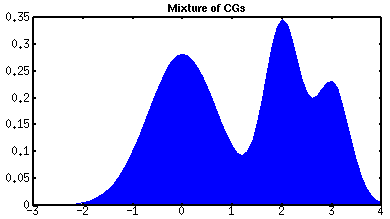
Beispiel für eine Aposteriori-Verteilung die sich aus drei gewichteten Normalverteilungen (CGs ohne Tail-Variablen) zusammensetzt:
| P(x)
= |
0.5
× Norm(0, 0.5) + 0.3 × Norm(2, 0.125) + 0.2 × Norm(3, 0125) |
Berechnen der
A-Posteriori-Verteilung kontinuierlicher Knoten
- Für das Cluster Ci welches mit der Eliminierung von Xi selbst entstanden ist wird eine Kopie seines LP-Potenzials in den Postbag abgelegt.
- Es wird eine modifizierte Push-Operation
durchgeführt, mit der diese Kopie in Richtung
Root-Cluster weitergereicht wird, bis ein rein
diskretes Cluster (Boundary-Cluster) erreicht wird:
- Dazu wird zunächst das aktuelle Cluster Ca gleich dem Ausgangscluster Ci gesetzt.
- Wenn es ein hybrides Elterncluster Cp von Ca gibt, dann lege eine (an die Größe der LP-Potenzial-MDTCG's von Cp angepasste) Kopie des Postbag-MDTCG's von Ca in den Postbag von Cp.
- Wenn Cp noch "aktiv" ist, d.h. wenn für den Eliminierungsknoten Xp von Cp noch keine Evidenz eingebracht wurde:
- Führe die Exchange-Operation
auf allen CGs des LP-Potenzials mit allen
entsprechenden CGs des Postbags von Cp
aus, wobei hier nur die Postbag-CGs wirklich
verändert werden dürfen!
- Der Postbag von Ca kann nun wieder geleert werden.
- Setze Ca := Cp und fahre fort bis ein Boundary-Cluster erreicht wird
- Ist ein diskretes Boundary-Cluster Cp erreicht worden9), so enthält das Postbag-MDTCG von Ca nur noch "unbedingte" CGs (also solche ohne Tail-Variablen) mit Xi als Head-Variable. Das entspricht einer normalen Gauss- oder Normalverteilung über Xi. Für diese Normalverteilungen wird nun eine multidimensionale Gewichtstabelle berechnet, die für jede CG im Postbag-MDTCG einen Gewichtwert enthält, der sich aus der (entsprechend marginalisierten) Wahrscheinlichkeitstafel des diskreten Boundary-Clusters ergibt. Diese Gewichte werden zu der Postbag-MDTCG abgelegt10) und diese finale gewichtete Postbag-MDTCG stellt dann die gesuchte A-Posteriori-Verteilung des Knotens Ci dar. Es kommt also keine einzelne Normalverteilung, sondern eine "Mixture of Gaussians" heraus.
- Ist kein diskretes Boundary-Cluster erreicht worden, weil es sich um ein rein kontinuierliches Netz handelt, so wird stattdessen im letzten Schritt das Root-Cluster erreicht. Auch dort enthält der hier skalare Postbag-MDTCG die (unebdingte) Normalverteilung des Knotens Xi welche dann als die gesuchte A-Posteriori-Verteilung (mit dem Gewicht = 1) ebgelegt werden kann.
Man sieht das Verfahren ist
doch vergleichsweise aufwändig (auch Rechenintensiv)
und kann für sonst harmlose Strukturen bereits zu
Komplexitätsproblemen führen, da die
Eliminierungreihenfolge nicht frei wählbar ist und so
evtl. sehr viele diskrete Knoten in gemeinsame Cluster
gepackt werden. Diese Problem betrifft jedoch nur echte
hybride Netze, nicht jedoch rein kontinuierliche Netze, die
mit dem Verfahren auch berechnet werden können. In
jedem Fall muss aber für jede eingebrachte Beobachtung
bezüglich eines kontinuierlichen Knotens bereits
(zumindest teilweise) über den hybriden Teil des
Elimination-Trees itertiert und MDTCG-Größenanpassungen
und
CG-Modifikationen (Exchange, Set-Tail) durchgeführt
werden. Fast dasselbe passiert nochmal für jeden Knoten
für den man die A-Posteriori-Verteilung berechnen will.
Beides sind in diskreten Junction-Trees vergleichsweise
einfache und vor allem lokale Operationen. Dafür muss
in diskreten Junction-Trees (wie im diskreten Teil des
Strong-Elimination-Trees) einmal, in der Propagations-Phase,
eine volle Message-Passing-Sequenz (in der üblicher
Weise über jeden Seperator zweimal gesendet wird)
über die gesamte Struktur durchgeführt werden, was
im hybriden Teil zwar wegfällt, den Aufwand beim Setzen
der Evidenz und beim Berechnen der A-Posteriori-Verteilungen
aber nicht wettmachen kann. Trotzdem kann es den
vergleichsweise einfachen Sampling-Verfahren überlegen
sein (ich persönlich traue den Sampling-Verfahren ja
immer nur sehr bedingt über den Weg :-)
Weitere exakte Verfahren:
Ein anderes exaktes Verfahren ist das in [2] beschriebene. Dieses hat dieselben Einschränkungen bezüglich der Struktur und Verteilungsarten wie das im letzten Abschnitt beschriebene Vefahren und baut ebenfalls auf einem Strong-Elimination-Tree (der hier dann noch zu einen Strong-Junction-Tree aggregriert wird) auf und kann somit prinzipiell in dieselben Komplexitätsprobleme laufen, die bereits für den Ansatz von Cowell beschrieben wurden. Darüberhinaus benötigt der Algorithmus mehr Operationen auf CGs und scheint insgesamt komplexer zu sein. So können Conditional Gaussians hier mehr als eine Head-Variable haben, womit auch die Faktoren nicht mehr in einem Vektor abgebildet werden können sondern in eine Matrix benötigt wird. Ebenso ist die Varianz einer CG nicht mehr nur ein Skalarer Wert. Näheres kann in [1] nachgelesen werden.
Dynamische Netze:
Noch ein Hinweis zu dynamische Netzen. Die diesbezüglichen Verfahren sind natürlich anwendbar, wenn man sich auf solche Verfahren beschränkt die auf einem "entrollten" Netz arbeiten, also einem Netz welches bereits alle benötigten Zeit-Scheiben enthält. Verfahren die einen Junction-Tree, oder hier einen Strong-Elimination-Tree, nur jeweils für ein aktuell betrachtetes Zeitfenster aufbauen, können nicht ohne Weiteres adaptiert werden, da in dem vorgestellten Verfahren Cluster nicht in demselben Maße über Separatoren getrennt sind, sondern Cluster-Potenziale immer mindestens über einen Teilbaum in Richtung des Strong-Root-Clusters "verschickt" und dabei umgerechnet werden müssen.
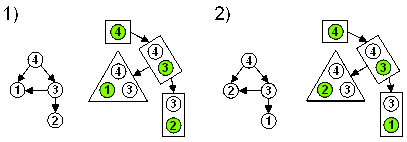
| 1) |
Die zweite
Nebenbedingung (nach dem "und") wird in [1]
so nicht genannt, scheint aber notwendig zu sein,
wie das folgende Beispiel verdeutlicht, in dem zwei
unterschiedliche Eliminierungsreihenfolgen
gewählt wurden, die aber zum selben
Elimination-Tree führen. Im linken Beispiel ist
C3 nur Teilmenge von C1,
während das zuletzt erzeugte Kind-Cluster C2
ist (die Cluster sind jeweils nach ihrem
Eliminierungsknoten (grün) bennant).
Keinesfalls kann hier C2
als Aggregations-Cluster genommen werden, da sonst
die Running-Intersection-Eigenschaft verletzt
würde (Knoten 4 käme, im dann mittleren
Cluster C2
nicht vor, aber in beiden angrenzenden Clustern C1
und C4,
wobei man hier zusätzlich annehmen muss, dass C4
weitere Knoten enthält um nicht bereits vorher
aggregiert worden zu sein). Im rechten Beispiel ist
es genau umgekehrt, so dass C3
hier tatsächlich Teilmenge des zuletzt
erzeugten Kind-Clusters C2
ist. Auch die zweite Bedingung ist notwendig - so
können z.B. (nur) die Knoten 3 und 4 diskret
und damit das Cluster C3
rein diskret sein - es ist jedoch nicht weiter
aggregierbar, da es zwar Teilmenge von C1
(links) bzw. C2
(rechts) ist, diese aber nicht rein diskret sind.
|
||
| 2) | wobei Knoten-MDTCG (sowie später auch Postbag-MDTCG) gleich, mittels der Reshape-Operation, an die für das LP-Potenzial des Zielclusters ggf. benötigte größere Größe (bedingt durch die evtl. höhere Anzahl der diskreten Knoten im Cluster verglichen mit den diskreten Elternknoten des Knotens) angepasst werden sollte, indem die CGs entsprechend für die noch nicht enthaltenen Dimensionen kopiert werden. | ||
| 3) |
wobei man sich
hier das oben beschriebene Anpassen des MDTCG
an das konkrete Cluster noch sparen, kann, da die
Postbags ohnehin an andere Cluster weitergereicht
werden und dann eine entsprechende Anpassung
nötig wird. |
||
| 4) |
enthält die Liste auch die diskreten Cluster, kann bei erreichen des ersten solchen Clusters abgebrochen werden, da alle nicht rein diskreten vor allen rein diskreten Clustern entstanden sind | ||
| 5) |
in der topologischen Reihenfolge steht ein Knoten X vor allen seinen Nachfahren - und das muss für alle Knoten X gelten | ||
| 6) |
die Head- und Tail-Variablen sind für alle CGs in einem MDTCG immer dieselben! | ||
| 7) |
dieses Cluster muss existieren und es muss ein hybrides, also nicht rein diskretes, Cluster sein, sonst stimmt was nicht... | ||
| 8) |
soetwas wie
Soft-Evidenz ist für kontinuierliche Knoten
nicht vorgesehen, d.h. die Evidenz ist ein skalarer
Wert wie z.B. 4.764m |
||
| 9) |
für rein
kontinuierliche Netze gibt es kein solches Boundary
Cluster und dieser Schritt entfällt einfach |
||
| 10) |
implementierungstechnisch kann man z.B. vorsehen dass jede CG selbst ihren Gewichtswert hält, der sonst normalerweise = 1 gesetzt ist |
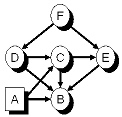
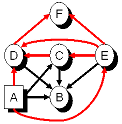
Das folgende (aus [1]
übernommene) hybride Beispielnetz hat nur einen diskreten
Knoten. Daher kann der Strong-Semi-Elimination-Tree auch nur
ein rein diskretes Cluster enthalten, welches diesen einzigen
Knoten diskreten Knoten A
enthält und somit auch gleichzeitig das
Strong-Root-Cluster, sowie das Boundary-Cluster für alle
hybriden Cluster ist. Außerdem ist dadurch der
Strong-Elimination-Tree auch bereits ein
Strong-Semi-Elimination-Tree, da keine Aggregation von rein
diskreten Clustern in sie vollständig enthaltende rein
diskrete Cluster möglich ist. Gut zu erkennen ist aber,
dass es kein echter Junction-Tree ist, da nur zwei "echte"
Cliquen ({A,B,C,D,E} und {C,D,E,F}) enthalten sind und alle
anderen Cluster Teilmenge einer dieser beiden Cliquen sind.
Der Strong-Semi-Elimination-Tree ist übrigens ein anderer
als der in [1]
präsentierte, da der dort gezeigte, meiner Meinung nach
den kleinen didaktischen Nachteil hat, garkein "echter" Baum,
sondern lediglich ein "Chain-Graph" zu sein in dem alle
Cluster in Reihe "geschaltet" sind.
 |
|
 |
|
Hybrides Bayes'sches Netz mit einem diskreten Knoten A und fünf kontinuierlichen Knoten B, C, D, E, F |
Ein BN, dass dieselbe gemeinsame
Wahrscheinlichkeitsverteilung über alle
Knoten repräsentiert, in dem jedoch einige
Kanten umgedreht bzw. hinzugefügt wurden
|
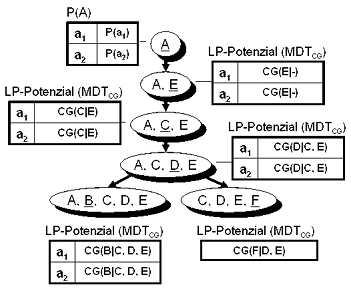 |
|
Ein
möglicher Strong-Semi-Elimination-Tree nach
der Initialisierung (alle LP-Potenziale sind
gefüllt, alle Postbags sind leer)
|
Nach der Initialisierung und
vor der Collect-Postbags-Phase haben die kontinuierlichen
Cluster folgende LP-Potenziale und Postbags:
Nach der Collect-Postbag-Phase haben die Cluster dann die in der obigen Abbildung gezeigten LP-Potenziale (und alle Postbags sind leer)
 |
A,B,C,D,E: |  |
A,C,D,E: |  |
C,D,E,F: |  |
A,C,E: |  |
A,E: | ||||||
 |
|||||||||||||||
| LP-Potenzial: |
 |
|
 |
- |
 |
|
 |
- |
 |
- |
|||||
 |
|||||||||||||||
| Postbags: |
 |
- |
 |
|
 |
|
 |
- |
 |
- |
|||||
 |
 |
||||||||||||||
 |
 |
 |
|
 |
 |
||||||||||
Nach der Collect-Postbag-Phase haben die Cluster dann die in der obigen Abbildung gezeigten LP-Potenziale (und alle Postbags sind leer)