
BAYES'SCHE NETZE
PROBABILISTISCHE NETZE
(Bayesian Networks / Probabilistic Networks / Causal Belief Networks)
Bei Baye'schen Netzen können sowohl die Struktur, als auch die bedingten Wahrscheinlichkeitstafeln "gelernt" werden. Versuchen wir zunächst letzteres: Wenn ein Datensatz vorhanden ist, in dem immer alle Merkmale des BNs beobachtet wurden reduziert sich die Bestimmung der bedingten Wahrscheinlichkeitstafeln (CPT's) auf ein Auszählen und Normieren.
Z.B. um die CPT eines Knoten B mit dem einzigen Elternknoten A zu bestimmen:
Die Probleme fangen an, wenn die Daten lückenhaft
sind,
d.h. wenn
für einzelne Merkmale der Zustand manchmal oder immer
unbeobachtet
geblieben ist. Fehlen nur in wenige Fällen
Beobachtungen kann man
u.U. nur mit dem vollständigen Teil der Daten arbeiten,
wobei man
natürlich die Information verliert die im
unvollständigen
Teil der Daten enthalten ist. Sind aber
einzelne Merkmale immer unbeobachtet oder fehlt in den
meisten
Fällen mind.
die Beobachtung eines Merkmals muss offensichtlich anders
verfahren
werden.
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Datensatz mit zeitweise fehlenden
Beobachtungen für A und B und einem
immer unbeobachteten Merkmal C
Hierfür hat sich der Expectation-Maximization-Algorithmus (EM), bzw. Baum-Welch-Algorithmus bewährt. Diese allgemein zur Schätzung von Wahrscheinlichkeitsverteilungen gebräuchliche Methode ist in BNs (jedenfalls solchen die über ein Junction-Tree-Verfahren rechnen) relativ leicht anzuwenden. Dazu werden die CPTs zunächst mit zufälligen Werten initialisiert (keine Verteilungen, die eine Unabhängigkeit der Merkmale darstellen - wie z.B. eine Gleichverteilung - benutzen!).
- Danach werden im Expectation-Step die Beobachtungen des Datensatzes (Zeilen) einzeln im Netz propagiert. Zu einer anfangs mit 0 initialisierten Tafel E(X,pa(X)) für jeden Knoten X wird nun die berechnete A-Posteriori-Verteilung dieses Knotens und seiner Eltern P'(X,pa(X)) addiert (addiert wird analog zum Multiplizieren / Dividieren von Wahrscheinlichkeitstafeln). Die Tafel P'(X,pa(X)) ist aus der (einer) Home-Clique zu erhalten.
- Im Maximization-Step wird die Erwartungstafel E(X,pa(X)) in die neue CPT P(X|pa(X)) umgewandelt, indem entsprechend normiert wird. Diese Umwandlung ist analog zu dem Verfahren für vollständige Daten (s.o).
Nun noch kurz ein Absatz der eigentlich an den Anfang
gehört hätte, aber ich will ja niemanden
verschrecken. Es
wird nämlich praktisch immer mit stark vereinfachenden
Annahmen
gearbeitet:
Eine solche vereinfachende Grundannahme ist,
dass das Fehlen einer Beobachtung unabhängig vom
tatsächlichen
Zustand ist. Das ist keineswegs immer der Fall. So
könnte z.B. das
Fehlen des Wertes eines Seismographen daher rühren,
dass ein
besonders starkes Erdbeben das Gerät selbst
beschädigt hat,
somit der fehlende Wert auf ein starkes Beben hindeutet und
keineswegs
unabhängig vom Beobachtungswert (Erdbebenstärke)
ist. Eine
weitere häufige Annahme (in statischen BNs) ist
die der Unabhängigkeit der einzelnen Beobachtungen
(Zeilen im
Datensatz).
Auch dafür kann man schnell ein Gegenbeispiel finden:
z.B. sind in
Zeitreihen, jedenfalls solchen mit kurzen
Aufzeichnungsintervallen,
aufeinanderfolgende Beobachtungen nicht unabhängig (das
ist ja
z.T. gerade der Witz einer Zeitreihe). Daher vereinfachen
solche
Annahmen zwar das Leben, sind aber u.U. zu einfach
gedacht
und müssen ggf. revidiert werden.
Gleich vorne weg gesagt sei, dass hierfür die Interpretation der Kanten als kausale Abhängigkeit zwischen einer Ursache und einer Wirkung aufgeweicht werden muss. Verschiedene Netzstrukturen können dieselbe zugrundeliegende Wahrscheinlichkeitsverteilung
P(X1,...,XZ)
kodieren (s.a. Kettenregel). Solche äquivalenten Netzstrukturen sind aber damit anhand von Daten nicht zu unterscheiden. Es geht also bei der Struktur-Suche letztlich "nur" darum die zugrundeliegende Wahrscheinlichkeitsverteilung möglichst gut abzubilden. Eines, wenn nicht das Hauptproblem aller Lernverfahren, die die Modellkomplexität (hier gegeben durch die Struktur) variieren ist die Frage der Vermeidung von Overfitting und Underfitting.
- Underfitting: Das gefundene Modell ist schlicht zu einfach um die vorhandenen Abhängigkeiten abzubilden.
- Overfitting: Das Lernverfahren überinterpretiert zufällige Schwankungen als Abhängigkeit. Da solche Schwankungen dann naturgemäß von Datensatz zu Datensatz andere sind funktioniert das Modell nur auf dem gelernten Datensatz gut, auf neuen Daten jedoch schlechter, als ein Modell das solche Scheinabhängigkeiten nicht enthält.
In realen Daten werden diese Bedingungen aber aufgrund zufälliger Schwankungen nie erfüllt; es scheinen alle Merkmale untereinander abhängig zu sein. Würde man also direkt mit dieser Definition arbeiten, um die Netzstruktur zu bestimmen, dann würde dies meist in einem (fast) vollständig verbundenen Graphen resultieren (und damit im extremsten Overfitting).
Dieses muss vermieden werden. Eine Möglichkeit dazu bietet das in [1] gezeigte Verfahren, dass nun dargestellt wird (die recht umfängliche Herleitung im Kasten unten kann zunächst auch übersprungen werden).
Die bedingten Wahrscheinlichkeiten des BN sind
letztlich die Parameter
mit denen die Wahrscheinlichkeitsverteilung abgebildet
wird. Man will diese Parameter so wählen, dass
genau diese Einstellung bei den gegebenen Daten die
wahrscheinlichste ist, d.h. man will P(θ1,...,θM|Data)
maximieren, wobei die θ's
("teta")
die
Parameter und Data die Daten sind. Nach der Bayes'schen
Formel gilt:
| P(θ1,...,θM|Data) = |
P(Data) |
Wie sich (gleich) zeigen wird sind unter bestimmten
Annahmen P(θ1,...,θM|Data),
P(θ1,...,θM)
und P(Data|θ1,...,θM) direkt
bestimmbar. Alle Wahrscheinlichkeitsverteilungen
müssten
eigentlich
zusätzlich die Struktur im Gegeben-Teil
aufführen, da
die Netz-Struktur für die zu bestimmenden
Parameter verantwortlich
ist (aus Platzgründen wurde darauf aber
verzichtet). Durch
Umformung
kann P(Data) bzw. eben P(Data|Struktur)
bestimmt
werden. Eigentlich gesucht ist aber ein Maß
für P(Struktur|Data), um
die wahrscheinlichste Struktur bei gegebnen Daten zu
finden.
Wiederum nach Bayes gilt:
| P(Struktur|Data) = |
P(Data) |
Da der Datensatz fest gegeben ist handelt es sich bei
1/P(Data)
lediglich um einen Normierungsfaktor, der
vernachlässigt werden
kann,
da die Größer-Kleiner-Beziehung davon
unbeeinträchtigt
bleibt. Die A-Priori-Wahrscheinlichkeit einer Struktur
ist schwierig zu
bestimmen. Es geht letzlich darum Modelle von
geringerer
Komplexität
(weniger Parameter) zu bevorzugen.
Ein Vorschlag lautet:
| P(Struktur) = e | -B/2 log N |
mit B=Anzahl freier Parameter und N=Anzahl BeobachtungenEs ist aber häufig so, dass gute Ergebnisse erzielt werden, wenn diese Größe vernachlässigt wird.
Es bleibt dann die sogenannte Likelihood:
P(Data|Struktur)
zu maximieren. Diese Art der Maximierung von P(S|Data) indem eigentlich P(Data|S) maximiert wird nennt man daher auch Maximum-Likelihood-Schätzung (wobei S nicht zwingend eine Struktur sein muss).
Nun aber der Reihe nach zu den einzelnen
Größen...
Für einen Parameter θ,
der die
Wahrscheinlichkeit beschreibt bei einem Münzwurf
"Kopf" zu werfen
gilt z.B.:
| P(Data|θ) = θ | kopf | (1-θ) | zahl |
wobei kopf bzw. zahl die Anzahl der Würfe im Datensatz ist bei denen "Kopf" bzw. "Zahl" geworfen wurde.Dieses gilt so nur wenn die einzelnen Würfe (Beobachtungen) unabhängig voneinander sind, was im weiteren vorausgesetzt wird. Der Parameter θ selbst besitzt eine Verteilung. Angenommen man hat verschiedene Datensätze (von Münzwürfen mit derselben Münze) und schätzt das θ aus jedem Datensatz einzeln, dann werden die Schätzungen variieren.
Diese Verteilung θ's kann durch die Beta-Verteilung beschrieben werden:
| P(θ) = P(θ|αk, αz) = norm θ | αk | (1-θ) | αz |
Wobei αk und αz ("alpha") die Hyperparameter der Beta-Verteilung sind, sie geben eine Art Vorwissen über die Verteilung an (entsprechend den Anzahlen kopf und zahl, die das aus den den Daten gewonnene Wissen darstellen). Die Kurzschreibweise P(θ) vernachlässigt diese Parameter.Der Normierungsfaktor norm ist gegeben durch:
| norm = |
Γ(αk) Γ(αz) |
Die Γ(x)-Funktion ("gamma") ist die stetige Fortsetzung von (x-1)! ("x-1 Fakultät"), also auch für nicht ganzzahlige Werte definiert.Unter der Annahme dass es sich um eine konjugierte Verteilung handelt ergibt sich die Verteilung, wenn Daten in der Form neuer Beobachtungen hinzukommen zu:
| P(θ|Data) = norm θ | αk+kopf-1 | (1-θ) | αz+zahl-1 |
mit
| norm = |
Γ(αk+kopf) Γ(αz+zahl) |
Dabei ist:Eine Verteilung ist konjugiert, wenn die Verteilung nach dem Bekanntwerden neuer Daten weiterhin aus derselben Familie ist - es sich hier also nach wie vor um eine Beta-Verteilung handelt.
- α = αk + αz
- kopf, zahl die Anzahl der hinzugekommenen Beobachtungen in denen "Kopf" bzw. "Zahl" geworfen wurde
- N die Anzahl der hinzugekommenen Beobachtungen (=kopf+zahl)
Ein Maß für die Likelihood der
Struktur ergibt sich
nun, wie oben bereits angedeutet
aus:
|
Der interessante Punkt ist, dass sich alle Teile die
von θ
abhingen weggekürzt haben. Die Beta-Verteilung
gilt jedoch
nur für zweiwertige Merkmale, für Merkmale
mit mehr als zwei
Zuständen wird die Dirichlet-Verteilung
benutzt.
Dirichlet-Verteilung (konjugiert,
Vorwissen
und
Daten):
|
|
|
|
|
Es sind:Die Herleitung verläuft vollkommen äquivalent zu dem zuvor gezeigten Prinzip, sieht nur komplizierter aus, weswegen dieser Teil hier ausgelassen wird.
- θij = Parameter-Satz des i-ten Knoten Xi (θij = {θij1,...,θijri})
- ri = Anzahl der Ausprägungen von Xi
- Nijk = Beobachtungen in denen Xi im k-ten Zustand ist während sich die pa(Xi) in der j-ten Zustandskonfiguration befinden
- αijk = Vorwissen bezüglich der k-ten Ausprägung
- Nij = Nij1+...+Nijri
- αij = αij1+...+αijri
Es ergibt sich
schließlich
die Likelihood, die als Maß der
Struktur-Güte
benutzt
wird und die es dementsprechend zu maximieren gilt:
|
|
|
Γ(αij+Nij) |
|
Γ(αijk) |
Dabei geht:Besonders bemerkenswert an dieser Formel ist die Tatsache, dass sie separabel ist, d.h. für jeden Knoten Xi gegeben die Menge der Elternknoten pa(Xi) getrennt - unabhängig voneinander - berechnet werden kann. Verändert sich die Elternmenge eines Knotens, durch eine Änderung der Netzstruktur, so kann das neue P(Data|Struktur') einfach gebildet werden durch:Weiterhin ist:
- i über alle Knoten {X1,...,XZ},
- j über alle Zustandskonfigurationen der Elternknoten von Xi und
- k über die Zustände des Knotens Xi selbst.
- Nijk die Anzahl der Beobachtungen in denen Xi in Zustand k und pa(Xi) in der j-ten Zustandskonfiguration sind.
- αijk die das Vorwissen Beschreibende Größe für den Knoten Xi im Zustand k und pa(Xi) in der j-ten Zustandskonfiguration. Der Wert für αijk gibt praktisch das Gewicht des Vorwissens gemessen in Beobachtungsanzahlen an.
- Nij und αij sind marginale Werte, sie ergeben sich aus Nij = Nij1+...+Nijri bzw. αij = αij1+...+αijri
| P(Data|Struktur') = |
P(Di|Struktur) |
P(Di|Struktur') |
Dabei ist:Es müssen also lediglich die einzelnen Faktoren für jeden Knoten aufgehoben werden. Danach kann ausgehend von einer initialen Netzstruktur jeweils die Änderung einer einzelnen Kante vorgenommen werden, die die stärkste Verbesserung bewirkt, bis keine (durch eine einzelne Änderung) Verbesserung mehr zu erreichen ist (Greedy-Search). Dabei ist normalerweise jeweils nur ein Knoten betroffen, ein Sonderfall ist jedoch das Umdrehen einer Kante, welches die Elternmenge von zwei Knoten ändert. Trotzdem sollte dieses in einem Schritt und nicht als zwei getrennte Schritte (Kante löschen, Kante Einfügen) modelliert werden, da kaum Anzunehmen ist, dass das Löschen einer solchen Kante im ersten Schritt eine Verbesserung bewirkt, was aber nötig wäre damit diese Aktion ausgeführt werden kann. Mit einem einem Greedy-Search-Verfahren, dass immer nur einen Schritt voraus plant kann natürlich i.a. nicht sichergestellt werden, dass das globale Optimum - die beste Netzstruktur gefunden wird.
- Struktur die alte und Struktur' die neue geänderte Netzstruktur,
- P(Di|Struktur) bzw. P(Di|Struktur'), der alte bzw. neue Einzelfaktor des Knotens Xi.
Problematisch ist aber insbesondere auch die Wahl des
Vorwissens (αijk's).
Anstatt
jedes αijk
einzeln anzugeben ist es sinnvoller ein Bayes'sches Netz
aufzustellen,
dass das Vorwissen (eines Experten) repräsentiert. Aus
der Home-Clique
eines Knotens Xi
im
Junction-Trees
kann P(Xi,pa(Xi))
gewonnen werden (u.U. durch Marginalisierung über die
übrigen
Merkmale der Clique). Ist die zu bewertende Netzstruktur
nicht dieselbe
wie jene, die das Vorwissen repräsentiert, so
differieren für
mind. einen Knoten die Elternmengen, d.h. im Junction-Tree
zum
"Vorwissen-BN"
existiert nicht unbedingt eine Home-Clique bezüglich
des zu
bewertenden
BN's. Z.B. eine Y-Propagation
liefert dennoch die gesuchte Tafel P(Xi,pa(Xi)).
Nun gilt:
αijk = P(Xi, pa(Xi)) USS
USS (User-Sample_Size) gibt ein Gewicht des Vorwissens in Beobachtungsanzahlen an. USS=1000 würde demnach bedeuten, dass das Vorwissen ein Gewicht hat als sei es aus einem Datensatz mit 1000 Beobachtungen gewonnen worden.Alternativ kann auch ein Vorwissen-Datensatz aus dem Vorwissen-BN mittels Daten-Sampling erzeugt werden.
Passen Vorwissen und Daten relativ gut zueinander liefert
das
Verfahren
recht gute Ergebnisse. Weichen Vorwissen und Daten stark
voneinander ab
liefert das Verfahren dagegen keine guten Ergebnisse. Es
zeigt sich
dementsprechend
auch, dass es keine gute Idee ist mangelndes Vorwissen wie
in der
Bayes'schen
Wahrscheinlichkeitsrechnung sonst üblich mittels Gleichverteilungen
bzw. Nicht-Informativen Verteilungen darzustellen.
Nicht
intuitiv
ist insbesondere die Tatsache, dass mit Vorwissen dass durch
ein kantenloses
Netz repräsentiert wird ein umso stärker
verbundener Graph
gelernt
wird je höher dieses Vorwissen gewichtet wird (USS).
Daraus entstand die Idee auch die αijk
aus den Daten zu bestimmen [5]. Die
Datensatzgröße
darf jedoch nicht überbewertet werden (Beobachtungen
dürfen
nicht
doppelt zählen). Daher wird ein Teilungsfaktor β
("beta") eingeführt:
Nijk = (1-β) Nijk* , αijk = β Nijk* , 0 < β < 1
Die Nijk* sind die ursprünglichen aus den Daten gewonnenen Werte (also das was vorher als Nijk bezeichnet wurde)Zusätzlich soll das Vorwissen aber den "konservativen" Part in der Berechnung übernehmen. Daher werden die αijk nicht (wie oben angedeutet) direkt aus den Nijk* erzeugt, sondern es werden erst die Parameter des noch unveränderten Netzes aus den Daten geschätzt und aus diesem BN, dann wie oben beschrieben die αijk erzeugt. Dabei ist dann USS = β N (N=Anzahl der Beobachtungen im Datensatz). Vorteil der Methode ist die Gewichtung über den Parameter β. Obwohl gegen kleine Veränderungen recht robust gilt i.a.: Je kleiner β desto mehr Kanten werden gefunden, da der "konservative" Part dann verschwindet. Werte um 0.1 bis 0.3 haben sich für die "β-Methode" bewährt.
Ähnlich gut funktioniert eine einfachere Methode, die in der Bewertungsformel alle αijk := 1 setzt (die αij ergeben sich entsprechend). Allerdings kann mit der "α=1-Methode" keine Gewichtung vorgenommen werden, die es erlauben würde die Kantenanzahl zu regulieren.
|
Beobachtungsumfang
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Gesamt-Trefferquote der beiden Verfahren, bei verschiedenen Netzstrukturen mit drei Knoten. Die Daten wurden aus einem vorgegebenen BN gesampelt. Alle zum vorgegebenen Netz äquivalenten Ergebnisse sind "Treffer"
Es existieren auch noch andere
Bewertungs-Fomeln
wie die Bayesian Quality (BQ), das Bayesian
Information
Criterion
(BIC) oder die MDL-Quality [6]:
|
|
|
log |
(Nij + ri -1)! |
+ |
|
|
|
|
|
Nijk log |
Nij |
|
|
|
|
Nijk log |
Nij |
|
Wiederum geht:f(N) ist eine von der Datensatzgröße N abhängige Funktion. Mit f(N) = 1/2 log N ergibt sich die MDL-Quality als Spezialfall aus dem Bayesian Information Criterion (BIC)
- i über die Knoten {X1,...,XZ}
- j über die qi Elternzustandkombinationen
- k über die ri Zustände von Xi
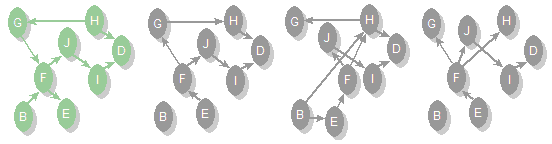
Beispiel-Ergebnisse des Lernverfahrens mit verschiedenen Bewertungskriterien:
wahres Netz (Referenz), β-Methode, α=1-Methode, BIC (von links)
Diese Kriterien sind ebenfalls separabel, d.h. für jeden Knoten einzeln berechenbar, jedoch ergibt sich der Gesamtwert aus der Summe (nicht dem Produkt der Einzelwerte). An dieser Stelle sollte aber erwähnt werden, dass wegen der extrem kleinen Werte zweckmäßiger Weise auch nicht P(Data|Struktur) sondern log P(Data|Struktur) berechnet wird. Der Logarithmus wird dabei so weit wie möglich in die Formel hineingezogen, so dass mit der log-gamma-Funktion gearbeitet wird. Dadurch werden aus den Produkten auch hier Summen (und aus den Brüchen Subtraktionen). Auch die letzten drei Kriterien (BQ, BIC, MDL) können mit log(a/b) = log(a)-log(b) und unter Verwendung von (x-1)! = Γ(x) noch umgeformt werden.
Für alle Verfahren gilt, dass sie mit den Verfahren zum Umgang mit fehlenden Daten, wie dem EM-Algorithmus kombiniert werden müssen, wenn die Daten unvollständig sind.
Angenommen man fragt sich ob man den Frostschutz des Auto-Kühlers erneuern soll, oder ob man sich darauf verlässt, dass der Frostschutz noch ausreicht. Die Kosten des Frostschutzmittels betragen 5,- / die Kosten, wenn das Kühlwasser einfriert und den Motor beschädigt betragen 5000,-. Den Frostschutz wird man dabei normalerweise nur dann als Kosten anrechnen, wenn er überflüssiger weise nachgefüllt wird (anders wäre es u.U. wenn man sich fragt ob man das Auto ganz abschaffen soll).
Kosten-Matrix:
|
|||||||||||||||
Ein BN liefert eine Vorabschätzung ob der Frostschutz
noch reicht
oder nicht. Diese Schätzung lautet:
|
P(Frostschutz=reicht|Evidenz)
=
0.99
P(Frostschutz=reicht nicht|Evidenz) = 0.01 |
Daraus ergeben sich die erwarteten
Kosten:
|
|||||||||||||||||||
Bei gleichen Kosten für beide Fehlerfälle würde man sich aufgrund der BN-Schätzung für nicht nachfüllen entscheiden. So liegen aber trotz der relativ eindeutigen BN-Schätzung die Erwartungskosten für diese Entscheidung mehr als 10 mal höher als dafür (wahrscheinlich überflüssiger weise) neuen Frostschutz nachzufüllen. Man sieht, dass es die Wahrscheinlichkeitsangabe sehr leicht macht solche Kostenfunktionen zu berücksichtigen. Teilweise werden sie in der Form zusätzlicher Knoten direkt in das BN integriert.
- Die Knoten des BN's werden in einer Liste derart sortiert, dass für jeden Knoten X alle Elternknoten pa(X) vor X in der Liste stehen.
- In der Reihenfolge dieser Liste wird der Zustand jedes Knotens zufällig entsprechend der zugrundeliegenden Verteilung P(X|pa(X)) festgelegt, wobei der/die ersten Knoten keine Eltern haben und für alle späteren die Elternzustände gegeben sind, weil sie bereits vorher bestimmt wurden. Die so gefundene Konfiguration aller Knoten ergibt schließlich eine Beobachtung des virtuellen Datensatzes.
- Der zweite Schritt wird solange wiederholt bis die gewünschte Anzahl von Beobachtungen im Datensatz enthalten ist.
Eines ist das Likelihood-Weighting-Sampling (LW-Sampling):
Ein weiteres ist das Gibbs-Sampling-Verfahren [3]:
- Zuerst muss eine mit der aktuellen Evidenz konsistente
Konfiguration
der
Merkmale gefunden werden. Das geschieht mit dem oben
beschriebenen
Verfahren.
Es muss also solange gesampelt werden bis eine solche
Konfiguration
gefunden
ist. Das kann aufwändig sein, weshalb unten noch eine
Aufweichung
dieser Bedingung beschrieben wird.
- Über die Bayes'sche Formel kann nun aus der Konfiguration der Elternknoten pa(X), der Kindknoten ch(X) und der Elternknoten der Kindknoten pa(ch(X)) (dem sogenannten Markov-Blanket, vgl. auch Abhängigkeitsstruktur (d-separation)) auf die bedingte Verteilung von X gegeben diese Konfiguration geschlossen werden, um daraus dann einen neuen Zustand zu sampeln. Dies wird für alle Knoten einmal ausgeführt um eine neue virtuelle Beobachtung dem Datensatz hinzuzufügen.
- Der zweite Schritt wird für einen virtuellen Datensatz mit N Beobachtungen N-1 mal ausgeführt (die erste Beobachtung entsteht ja schon durch Schritt 1)
Desweiteren kann man nach M erzeugten Samples wieder beim ersten Schritt anfangen (Re-Sample-In), um in andere Bereiche der Verteilung vorzustoßen, die bisher nicht erreicht wurden.