3D-Bezier-Surfaces

Bezier-Kurven und -Flächen

Einleitung (Bezier vs. B-Spline)

Diese Seite beschreibt meine anno 2003 vollführten ersten Versuche aus mehreren "Freiflächen" zusammengefügte dreidimensionale Objekte zu erstellen und zu rendern. Da ich zunächst nur einen sehr rudimentären Editor zur Verfügung hatte, habe ich versucht einen Ansatz zu finden, der mit möglichst wenigen Parametern auskommt. Dazu habe ich Bezier-Flächen verwendet, die jeweils durch 4x4 Kontrollpunkte definiert sind, wobei ich diese 4x4 Kontrollpunkte nicht direkt definiere, sondern aus 4 Eckpunkten ableite für die jeweils zusätzlich ein Normalenvektor gegeben ist (Punkt + Normalenvektor habe ich als Nadeln dargestellt). Diese Flächen lassen sich recht gut miteinander verbinden. Leider bleiben jedoch teilweise Kanten ("Knicke") an den Übergängen sichtbar. Inzwischen (2012) habe ich einen weiteren Ansatz benutzt, der B-Spline-Flächen verwendet. Dieser benötigt zwar mehr Kontrollpunkte (Parameter), dafür ist es aber möglich mehrere Flächen "nahtlos" zusammenzufügen. Der Teil zu den B-Spline-Flächen kann hier nachgelesen werden.

Bezier-Kurven

In diesem ersten Abschnitt geht es um Bezier-Kurven - also eindimensionale "geschwungene" Objekte, die sich in diesem Fall jedoch im dreidimensionalen Raum befinden.

Basics

Bezier-Kurven werden definiert durch einen Anfangs- (P1) und einen End-Punkt (P2), sowie durch eine Anzahl (0,1,...) von Zwischenpunkten. Abgesehen von dem "pathologischen" Fall, dass alle Punkte auf einer Linie liegen ("Bezier-Gerade") befinden sich nur Anfangs- und Endpunkt auf der Kurve selbst. Die Kurvengleichung ist ein Polynom, dessen Ordnung von der Anzahl der (Zwischen-) Punkte abhängt. Oft - und so auch hier - werden zwei Zwischenpunkte (Z12, Z21) verwendet. Interressant ist, dass die Linie von P1 nach Z12 der Tangente in P1 entspricht, entsprechendes gilt für die Linie P2 nach Z21 im Punkt P2.

Mit vier Kontrollpunkten (d.h. zwei Endpunkten und zwei Zwischenpunkten) ergibt sich ein Polynom 3. Grades.
In Matrix-Schreibweise:

                              | -1 3 -3 1 |   | P1 |
                              | 3 -6 3 0 |   | Z12 |
Bezier(t) = | t^3 t^2 t 1 | * | -3 3 0 0 | * | Z21 |
                              | 1 0 0 0 |   | P2 |

... oder wer's lieber so hat:

Bezier(t) =    (1 - t)^3 * P1
             + (3 * t * (1 - t)^2) * Z12
             + (3 * (t^2) * (1 - t)) * Z21
             + (t^3) * P2

Forward Differencing

Hilfreich, um die Berechnung zu Beschleunigen ist ein Verfahren namens "forward differencing". In aller Kürze heisst dass: Es wird solange differenziert bis man bei konstanten Termen angelangt ist (d.h. drei mal bei einem Polynom 3. Grades).

delta1 = Bezier(step) - f(0)
delta2 = (Bezier(2*step)-Bezier(step)) - delta1
delta3 = ( (Bezier(3*step)-Bezier(2*step)) - (delta2+delta1) ) - delta2

So kann man die Berechnung auf bloße Additionen zurückführen (und die kann der gemeine Rechner nunmal schneller als Multiplikationen/Divisionen):

initial Schritt i=0:
`Bezier(t = 0) =`	`P1`
Schritte i = 1...N:
`Bezier(t = i * deltastep) =`	`Bezier(t = (i-1) * deltastep) + delta1;`
`delta1 =`	`delta1 + delta2;`
`delta2 =`	`delta2 + delta3`

C++-Code zur Berechnung der Deltas...

Zusammenfügen von Kurven

Statt die Zwischenpunkte direkt anzugeben verwende ich hier ein Verfahren bei dem die Anfangs-/Endpunkte A und B, sowie zwei Normalenvektoren a und b (jeweils im 3D-Raum) festgelegt werden (siehe auch C++-Code)

Durch A, a bzw. B, b sind die Tangentialebenen:
Ea(x) : a*x = da und Eb(x) : b*x = db bestimmt, wobei da=a*A und db=b*B ("*" ist hier das Skalarprodukt).

Nun werden die Schnittpunkte A' und B' von Ea und B+a*t bzw. von Eb und A+b*t bestimmt.

In Richtung dieser Schnittpunkte - also auf den Geraden A->A' bzw. B->B' werden schließlich die Zwischenpunkte A'' und B'' bestimmt.

Als sinnvoller Abstand für |A-A''| bzw. |B-B''| hat sich 1/(3*cos(alpha)) * |A-B| erwiesen.
Dabei ist:

\|A-B\|	Abstand der Punkte A und B zueinander.
cos(alpha)	Winkel zwischen der Line A-B und der Line A-A' bzw. B-B'

Mit Hilfe dieser Berechnungsform lassen sich relativ einfach Bezier-Kurven aneinanderreihen, die eine "gute Fortsetzung" bilden, da sie in den gemeinsamen Punkten identische Tangenten (2D) / Tangentialebenen (3D) aufweisen.

Bezier-Flächen

In diesem Abschnitt geht es nun um Bezier-Oberflächen, also zweidimensionale geschwungene Objekte, wiederum im dreidimensionalen Raum.

Basics

Bezier-Oberflächen mit 4x4=16 Kontrollpunkten können mit Hilfe folgender Formel gebildet werden:

`Bezier(s,t) =`	`S * P * T`
S =	`\|-1 3 -3 1\|` `\| 3 -6 3 0\|` `\|s^3 s^2 s 1\| * \|-3 3 0 0\|` `\| 1 0 0 0\|`
P =	`\|P11 P21 P31 P41\|` `\|P12 P22 P32 P42\|` `\|P13 P23 P33 P43\|` `\|P14 P24 P34 P44\|`
T =	`\|-1 3 -3 1\| \|t^3\|` `\| 3 -6 3 0\| \|t^2\|` `\|-3 3 0 0\| * \| t \|` `\| 1 0 0 0\| \| 1 \|`

Analog zu Bezier-Kurven liegen im Allgemeinen nur die Eckpunkte (P11, P41, P14, P44) auf der Oberfläche selbst. Auch (insbesondere) für Bezier-Oberflächen bietet sich das Forward-Differencing an (siehe C++-Code)

Zusammenfügen von Flächen

Wie bei den Bezier-Kurven will ich nur die Eckpunkte (P11, P41, P14, P44) sowie einen Normalenvektor (N11, N41, N14, N44) pro Ecke festlegen. Dabei können auch zwei "benachbarte" Punkte inkl. Normalenvektoren identisch sein, was dann eine "dreieckige" Fläche ergibt).

Die Zwischenpunkte auf den Rändern (P21, P31, P42, P43, P12, P13, P24, P34) werden wie für die Bezier-Kurven bestimmt, da die vier Ränder der Bezier-Oberfläche auch identisch den Bezier-Kurven mit den jeweiligen vier Rand-Punkten einer Seite sind (z.B. P11, P21, P31, P41).
Da die Rand-Zwischenpunkte nur von den zwei Eckenpunkten der jeweiligen Seite abhängen ist auch gewährleistet dass zwei verschiedene Flächen mit je (mind.) zwei gemeinsamen Eckpunkten (also mind. einer gemeinsamen Seite) auch wirklich (ohne Lücke) aneinandergrenzen. Problematischer ist die Bestimmung der inneren Punkte (P22, P32, P23, P33). Diese sollen so gewählt werden, dass aneinandergrenzende Flächen einen möglichst stetigen Übergang bilden. Dieses ist nicht in Perfektion möglich; schon weil sich dazu die Wahl der Rand-Punkte an benachbarten Flächen orientieren müsste. Jedoch sind recht ansprechende Ergebnisse erzielbar. Und wenn man nach langer Zeit mal wieder alte Sachen hervorkramt, dann kann es passieren, dass man feststellt, dass man wiedermal den Wald vor Bäumen nicht gesehen hat und ein Verfahren gewählt hat, was eher zu kompliziert und außerdem noch in vielen Fällen instabil ist...

Trotzdem hier zunächst das "originale" Verfahren:
Um z.B. den Punkt P22 zu bestimmen wird zuerst das Lot von P12 auf die Linie P11-P14 gefällt. Dieses Lot bildet dann den Normalenvektor einer Ebene E12, die den Punkt P12 beinhaltet. Entsprechend wird auf der "anderen" Seite für den Punkt P21 verfahren, um eine weitere Ebene E21 zu bestimmen. P22 wird nun auf die Schnittlinie dieser beiden Ebenen gelegt. Und zwar so, dass P22 möglichst im rechten Winkel zu den Linien P11-P12 und P21-P22 liegt. Wobei sich wiederum die Distanzen zu den Nachbarpunkten in "vernünftigen" Grenzen halten müssen. Die unten dargestellte Methode scheint da einen ganz brauchbaren Kompromiss zu erziehlen.
Dieses Verfahren hat nun (offensichtlich :-) Probleme, wenn die beiden Ebenen E12 und E21 parallel liegen. Auch wenn P12 oder P21 sehr nahe bzw. sogar auf an den Linien P11-P41 bzw. P11-P14 liegen kommt es zu numerisch instabilen Berechnungen der Normalenvektoren für E12 und E21. Solche Instabilitäten treten z.B. dann auf wenn man eine glatte Fläche erzeugen möchte, oder den Abschnitt eines Zylinders.

Daher hier noch das abgewandelte Verfahren:
Statt die beiden Ebenen E12 und E21 und von diesen die Schnittgerade zu berechnen wird eine Mittellinie gebildet die von P11 ausgehend durch den Mittelpunkt zwischen P12 und P21 verläuft. Diese wird dann im Weiteren wie die Schnittgerade von E12 und E21 benutzt. Es ist weiterhin unbedingt sinnvoll P22 so zu legen, dass das die (gedachten) Verbindungen P22-P21 und P22-P12 möglichst rechtwinklig auf den Linien P11-P12 und P21-P22 steht.

Beide Methoden sind aber für das unten gezeigte Gesichtsmodell kaum zu unterscheiden, da hier die erwähnten Spezialfälle von Flächen die zu Instabilitäten in der ersten Variante führen nicht vorkommen. Was aber noch weit weniger sinnige Methoden so anrichten ist unten im Kapitel "Greatest Misses" zu bewundern. Eventuell hilft ja jemandem der C++Code weiter (der allerdings momentan nur die erste (instabile) Variante enthält)...


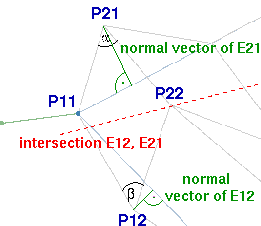
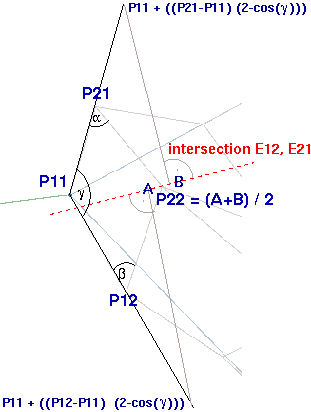
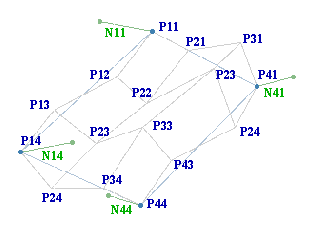
Berechnung von P22, wobei die Winkel alpha und beta möglichst rechtwinklig sein sollten.		Methode, um alpha und beta möglichst rechtwinklig zu bekommen: Verlängern der Linien P11-P12 und P11-P21 (abhängig vom Winkel gamma), von dort die Lote auf die Schnittlinie von E12 und E21 fällen und den Mittelpunkt der so gefundenen Punkte A und B bilden.


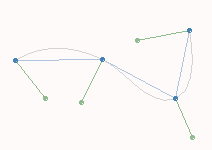
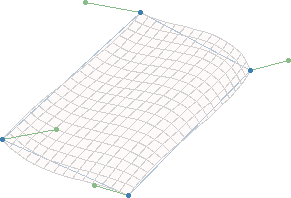
16 Kontrollpunkte, wobei alle nicht Eckpunkte mit Hilfe der Eckpunkte P11, P41, P14, P44, sowie der Normalenvektoren N11, N41, N14, N44 berechnet wurden		Gitter-Darstellung der resultierenden Bezier-Oberfläche

Gesichtsmodell

Durch das Zusammensetzen mehrerer Flächen lassen sich so mehr oder weniger komplexe Gebilde modellieren.


Die "Akupunkturnadeln" sind die Normalenvektoren (dies ist übrigens ein Snapshot eines Editors den ich gerade mit Java3D bastle)		Zur Verdeutlichung sind hier die Flächen jeweils mit einer zufällig gewählten Farbe eingefärbt worden

Greatest Misses

Auf der Suche nach dem "besten" (oder wenigstens einem brauchbaren) Verfahren gab's natürlich einige Irrungen und Wirrungen, wie man hier sieht (wobei sich aber nicht nur das Berechnungsverfahren, sondern auch das Gesichts-Modell geändert hat). Zum Rendern der Bilder wurde übrigens dasselbe Verfahren wie für die Fraktale verwendet - wen's interessiert der kann mal hier nachlesen.

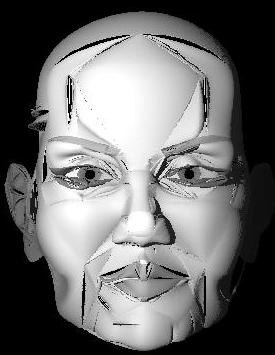
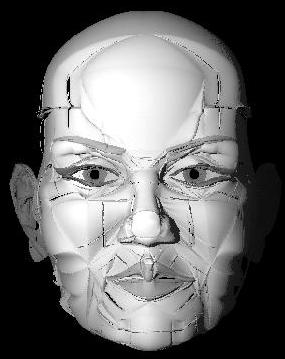
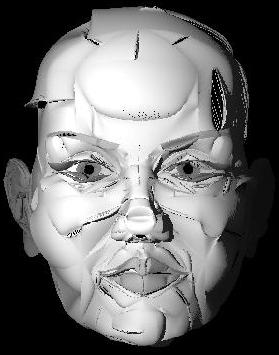
"Clown" Hilfspunkte liegen teilweise auf der "falschen Seite" der Eckpunkte	"Alien I" Versuche die Flächen aus einzelnen Bezier-Kurven aufzubauen führen zu "Instabilitäten" (Löcher, Risse, Kiemen, ...)	"Alien II" (Selbe Problematik wie bei "Alien I")	"Stubsnase" (Selbe Problematik wie bei "Alien I & II")
"Clown" Hilfspunkte liegen teilweise auf der "falschen Seite" der Eckpunkte	"Alien I" Versuche die Flächen aus einzelnen Bezier-Kurven aufzubauen führen zu "Instabilitäten" (Löcher, Risse, Kiemen, ...)	"Alien II" (Selbe Problematik wie bei "Alien I")	"Stubsnase" (Selbe Problematik wie bei "Alien I & II")
"Lochmaske" Erster Versuch mit echten Bezier-Flächen - die dreieckigen Flächen glänzen durch Abwesenheit, während die viereckigen sich unangemessen aufplustern (innere Hilfspunkte falsch berechnet)	"Papier" Versuch die Kanten zwischen Flächen zu bekämpfen indem die Flächen zunächst in kleinere Teilflächen aufgeteilt werden ... gescheitert ... (wäre aber prinzipiell nochmal eine Überlegung wert)	"Rund" Variationen der Abstände der Rand-Hilfspunkte zu den Eckpunkten: hier zu viel (2/3*cos(alpha)) / h)...	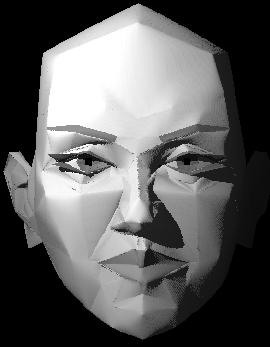"Eckig" ...und hier zu wenig (0.1*cos(alpha)) (vgl. Kapitel "Zusammenfügen von Bezier-Kurven")
"Lochmaske" Erster Versuch mit echten Bezier-Flächen - die dreieckigen Flächen glänzen durch Abwesenheit, während die viereckigen sich unangemessen aufplustern (innere Hilfspunkte falsch berechnet)	"Papier" Versuch die Kanten zwischen Flächen zu bekämpfen indem die Flächen zunächst in kleinere Teilflächen aufgeteilt werden ... gescheitert ... (wäre aber prinzipiell nochmal eine Überlegung wert)	"Rund" Variationen der Abstände der Rand-Hilfspunkte zu den Eckpunkten: hier zu viel (2/3*cos(alpha)) / h)...	"Eckig" ...und hier zu wenig (0.1*cos(alpha)) (vgl. Zusammenfügen von Bezier-Kurven)
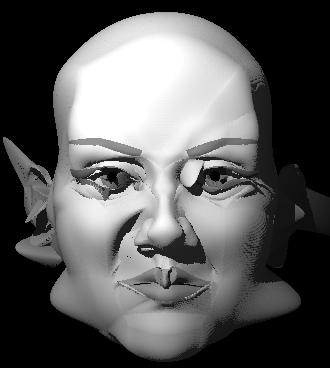
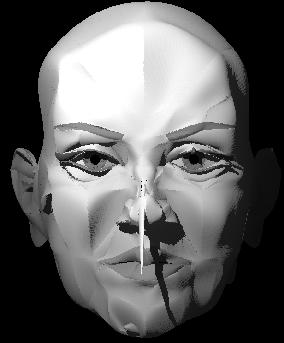
"Spocky" eine eher instabile Variante die inneren Hilfspunkte zu berechnen...	"Hexe" ...und gleich noch eine instabile Variante die inneren Hilfspunkte zu berechnen...	"Zerstreut" Wenn man die Punkte (durch einen Fehler in der Einleseroutine) komplett durcheinander wirft kann auch mal sowas rauskommen...	"Innenansichten" Das ist nun ausnahmsweise mal kein Fehler in der Bezier-Berechnung, sondern einfach die Innenansicht
"Spocky" eine eher instabile Variante die inneren Hilfspunkte zu berechnen...	"Hexe" ...und gleich noch eine instabile Variante die inneren Hilfspunkte zu berechnen...	"Zerstreut" Wenn man die Punkte (durch einen Fehler in der Einleseroutine) komplett durcheinander wirft kann auch mal sowas rauskommen...	"Innenansichten" Das ist nun ausnahmsweise mal kein Fehler in der Bezier-Berechnung, sondern einfach die Innenansicht
"Verflossen" Auch das ist kein Fehler bei der Bezier-Flächenberechnung sondern extreme/falsche perspektivische Verzerrungen. In diesem Fall liegt der Fluchtpunkt hinter der eigentlichen Gesichtsfläche, aber noch zwischen den Ohren...	"Jabba" ...und hier liegt der Fluchtpunkt sogar vor dem Gesicht, praktisch in der Nasenspitze.	"Zerknirscht" Ein weiterer Versuch die Glattheit dadurch zu erhöhen, dass die Flächen automatisch in kleinere Flächen unterteilt werden. Hier ist noch ein gravierender Fehler in der Normalen-Vektor-Berechnung enthalten.	"Stirnrunzeln" Und noch ein Versuch die Glattheit dadurch zu erhöhen, dass die Flächen automatisch in kleinere Flächen unterteilt werden. So sieht das - bis auf ein paar Artefakte - schon ganz gut aus. Allerdings werden die Stellen die eine Glättung besonders nötig hätten doch eher unruhig...
"Verflossen" Auch das ist kein Fehler bei der Bezier-Flächenberechnung sondern extreme/falsche perspektivische Verzerrungen. In diesem Fall liegt der Fluchtpunkt hinter der eigentlichen Gesichtsfläche, aber noch zwischen den Ohren...	"Jabba" ...und hier liegt der Fluchtpunkt sogar vor dem Gesicht, praktisch in der Nasenspitze.	"Zerknirscht" Ein weiterer Versuch die Glattheit dadurch zu erhöhen, dass die Flächen automatisch in kleinere Flächen unterteilt werden. Hier ist noch ein gravierender Fehler in der Normalen-Vektor-Berechnung enthalten.	"Stirnrunzeln" Und noch ein Versuch die Glattheit dadurch zu erhöhen, dass die Flächen automatisch in kleinere Flächen unterteilt werden. So sieht das - bis auf ein paar Artefakte - schon ganz gut aus. Allerdings werden die Stellen die eine Glättung besonders nötig hätten doch eher unruhig...
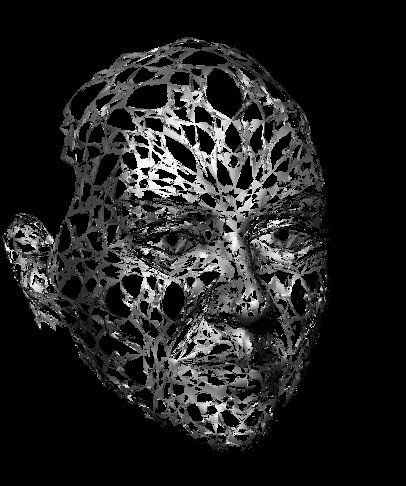
"Alien III" Der Kollege hat alle Normalenvektoren nach links bzw. rechts gezogen bekommen... (sehr unangenehm das)	"Alien IV" Und dieser Kollege hat nun alle Normalenvektoren nach oben bzw. unten gezogen bekommen... (auch nicht schön)	"Freddy" Hier sind einige Punkte verrutscht und die Normalenvektoren "verdreht", was doch zu kleineren Hautunreinheiten führt...	"Golfball" Automatisches Splitten der Bezierflächen, wobei aber (zu Testzwecken absichtlich) die Normalenvektoren des jeweils mittleren Punktes einer gesplitteten Bezierfläche auf (0,0,-1) gesetzt wurden
"Alien III" Der Kollege hat alle Normalenvektoren nach links bzw. rechts gezogen bekommen... (sehr unangenehm das)	"Alien IV" Und dieser Kollege hat nun alle Normalenvektoren nach oben bzw. unten gezogen bekommen... (auch nicht schön)	"Freddy" Hier sind einige Punkte verrutscht und die Normalenvektoren "verdreht", was doch zu kleineren Hautunreinheiten führt...	"Golf" Automatisches Splitten der Bezierflächen, wobei aber (zu Testzwecken absichtlich) die Normalenvektoren des jeweils mittleren Punktes einer gesplitteten Bezierfläche auf (0,0,-1) gesetzt wurden

Ergebnis

Und hier das vorläufige amtliche Endergebnis (eigentlich eher langweilig):

"Normal I" leichte Kanten sind nur noch dort zu erkennen wo Flächen relativ spitze Ecken haben; dieser Effekt ist mit diesem Ansatz nicht gänzlich vermeidbar, da eine Fläche jeweils vollkommen unabhängig von allen andern Flächen berechnet wird	"Normal II" ...nochmal dasselbe von der Seite	"Glanz I" ...mit mehr Glanz...	"Glanz II" ...und von der Seite
"Normal I" leichte Kanten sind nur noch dort zu erkennen wo Flächen relativ spitze Ecken haben; dieser Effekt ist mit diesem Ansatz nicht gänzlich vermeidbar, da eine Fläche jeweils vollkommen unabhängig von allen andern Flächen berechnet wird	"Normal II" ...nochmal dasselbe von der Seite	"Glanz I" ...mit mehr Glanz...	"Glanz II" ...und von der Seite
"Fraktal" ...und um das langweilige Ergebnis wieder etwas aufzupeppen hier mal das Abbild eines 3D-Julia-Fraktals...	"Sky" ...bzw. den blauen Himmel reflektierend (das dann auch noch perspektivisch verzerrt)...	"Checker" ...und nochmal kräftig verzerrt und ein Schachbrettmuster reflektierend...	"Sky-Checker" ...und nun noch eine letzte Spielerei: diesmal reflektiert das Gesicht wieder den blauen Himmel, ist aber außerdem mit einer Schachbrett-Textur überzogen
"Fraktal" ...und um das langweilige Ergebnis wieder etwas aufzupeppen hier mal das Abbild eines 3D-Julia-Fraktals...	"Sky" ...bzw. den blauen Himmel reflektierend (das dann auch noch perspektivisch verzerrt)...	"Checker" ...und nochmal kräftig verzerrt und ein Schachbrettmuster reflektierend...	"Sky-Checker" ...und nun noch eine letzte Spielerei: diesmal reflektiert das Gesicht wieder den blauen Himmel, ist aber außerdem mit einer Schachbrett-Textur überzogen

Java-Applikation

Leider nur die eher langweiligen Endprodukte kann man jetzt auch selbst erzeugen (übrigens auch die Über-Schrift)... zum Download geht's hier

Feedback

Freue mich über eure Meinungen, Anregungen, usw.
Mail-Adresse

.
Feedback-Formular