B-Spline-Surfaces (3D)

B-Spline(-ähnliche) Flächen

Einleitung (Bezier vs. B-Spline)

Dies ist die Fortsetzung meiner Versuche mit Bezier-Flächen ein Gesicht zu modellieren. Dieser erste Teil kann hier nachgelesen werden. Ich werde mich im Folgenden teilweise darauf beziehen. Meine damaligen Versuche hatten mehrere Probleme:

Ich hatte keinen halbwegs brauchbaren Editor und wollte daher mit möglichst wenigen Parametern (Einzelflächen) das Objekt (Gesicht) beschreiben. Bezier-Flächen schienen da gut geeignet.
Bezier-Flächen lassen sich aber dann doch nicht so schön zusammenfügen wie ich gehofft hatte (es bleiben Übergänge/"Knicke" zwischen den einzelnen Flächen sichtbar)

Inzwischen habe ich einen "3D-Editor" (s. hier) mit dem ich wesentlich mehr Punkte im Raum definieren kann. Dabei haben sich Punkte als leichter zu handhaben herausgestellt als die "Nadeln" (Punkt + Normalenvektor) mit denen ich die Bezier-Flächen definiert habe. Daher habe ich nach einem Algorithmus für diese Anforderungen gesucht:

Die Objekte sollen aus mehreren einzelnen Flächen bestehen können,
wobei jede Fläche durch eine Matrix aus N x M Kontrollpunkten definiert ist
angrenzende Flächen teilen sich dabei Punkte an ihren Rändern
die Objektoberfläche soll auch über die Grenzen einzelner Flächen hinweg glatt erscheinen

Im Folgenden versuche ich die Grundlagen zu vermitteln, soweit ich diese benötigt habe. Dies ist aber keine allgemeine Einführung in B-Splines oder sonstige Freiflächen!

B-Spline-Kurven

Seien P₁ und P₂ zwei Vektoren (bei mir immer 2D- bzw. 3D-Vektoren mit den Komponenten x, y bzw. x, y und z), dann erhält man mit

P = w₁ · P₁ + w₂ · P₂

alle Punkte P auf der Geraden durch die Punkte P₁ und P₂ geht und die zwischen P₁ und P₂ liegen.
Dabei gilt:

w₁ in [0..1] und
w₂ = 1 - w₁

außerdem gilt für die Multiplikation eines Vektors (hier P₁ und P₂) mit einem Skalar (hier w₁ und w₂), dass einfach jede der Komponenten eines Vektors P (P.x, P.y, Pz) mit dem Skalar w multilpiziert wird:

	(	P.x	)		(	w · P.x	)
w · P = w ·		P.y		=		w · P.y
		P.z				w · P.z

Für die Addition zweier Vektoren gilt, dass die jeweils entsprechenden Komponenten addiert werden:

	(	P₁.x + P₂.x	)
P₁ + P₂ =		P₁.y + P₂.y
		P₁.z + P₂.z

Lässt man die Bedingung dass w₁ aus [0..1] stammen muss weg, erhält man alle Punkte auf der Geraden durch P₁ und P₂ (also nicht nur die zwischen P₁ und P₂), aber das nur am Rande.

Lineare Kombination zweier Vektoren ergibt eine gerade Verbindung

Die Position auf der Geraden zwischen P₁ und P₂bezeichnen wir mit f, wobei f im Intervall [0...1] liegt und f=0 den Anfang der Geraden und f=1 das Ende der Geraden bezeichnet. Damit ist w₁(f) = 1 - f und w₂(f) = f.
Nehmen wir nun weitere Punkte und Gewichte hinzu:

P = w₁(f) · P₁ + w₂(f) · P₂ + w₃(f) · P₃ + w₄(f) · P₄ + ... + w_N(f) · P_N

Dabei ist nun aus dem Intervall [1...N] und f=1 bezeichnet den Anfang und f=N das Ende der Geraden¹⁾. Die zu den Kontrollpunkten P₁...P_N gehörenden Gewichte w₁...w_N hängen dann wie folgt von f ab:

w_i(f) = max(0, 1 - |f - i|)

Damit bekommt man eine Stückweise lineare Verbindung der Punkte P₁...P_N. Man beachte auch dass die Summe aller Gewichte immer gleich 1 ist:

∑ w₁(f)...w_N(f) = 1 (1)

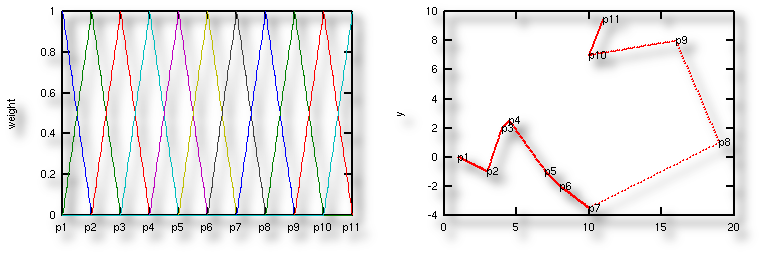Links: die Gewichte (an jeder Position ist die Summe aller Gewichte = 1)
Rechts: die resultierende "Kurve" (stückweise lineare Verbindung aller Punkte)

An einer Stelle f der Kurve sind jeweils max. zwei Gewichte ungleich 0 (ist f genau 1, 2, 3, 4, ... oder N, dann ist nur genau ein Gewicht ungleich 0 - nämlich "w_f"). Um nun eine "runde" Verbindung zu erhalten muss man die Gewichte anders definieren. Insbesondere sollen mehr als max. zwei Gewichte ungleich 0 sein können. Das heißt an einer Stelle f wirken sich mehr als nur zwei Punkte P_k und P_k+1 aus (wobei k hier dem auf die nächste Ganzzahl abgerundetem f entspricht). Die Summe aller Gewichte soll zwar weiterhin stets gleich 1 sein, jedoch kann man das jeweils durch Normierung erreichen:

w_i(f) = w_i(f)' / ∑ w₁(f)...w_N(f)

Man kann also Gewichte w_i' ... w_N' erstmal "unbeeindruckt" von dieser Bedingung (1) bestimmen.
Der lineare Ansatz, die Bereiche in denen ein Gewicht ungleich 0 ist einfach um den Faktor 2 zu strecken hat sich also nicht so zielführend erwiesen:

w_i(f) = max(0, 1 - |f - i| / 2)

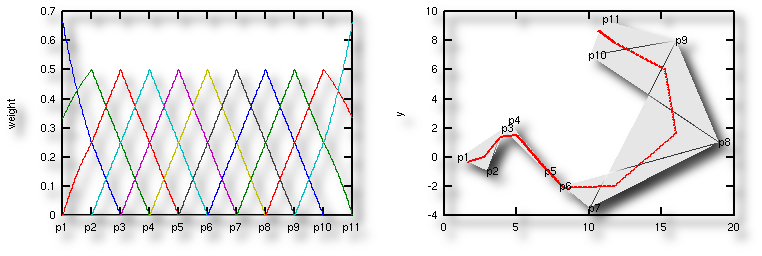Links: die normierten Gewichte (durch die Normierung an den Rändern "deformiert");
Rechts: die resultierende Kurve, die die Kontrollpunkte nicht mehr trifft, aber dummer Weise immer noch stückweise linear ist

Die Kurve bleibt innerhalb der konvexen Hülle (grau dargestellt)²⁾. Rund ist die Verbindung aber leider nicht. Warum? Einfach ausgedrückt: die Kombination linearer Funktionen bleibt immer linear.
Schon besser funktioniert Folgendes:

w_i(f) = cos(max(-2, min(2, f - i)) * pi / 2) + 1

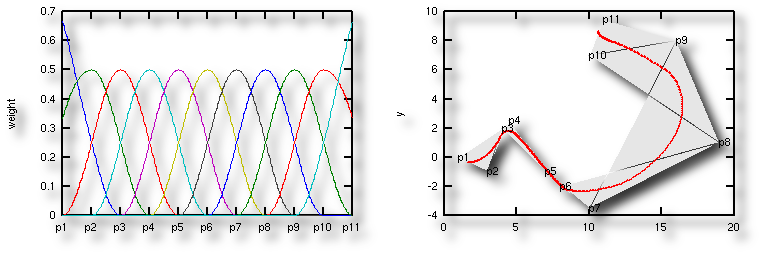Links: die normierten Gewichte, die auf einer abgeschnittenen Sinus- bzw. Cosinus-Funktion beruhen
Rechts: die resultierende Kurve: schon runder, aber noch nicht optimal...

Aber so schön rund, wie es sein sollte ist das auch noch nicht.
Noch besser funktioniert das hier:

w_i(f) = gauss(f, mean=i, var=0.6²)

Nur leider ist die Normalverteilungskurve ja nicht auf den Bereich [-2...2] begrenzt, sondern konvergiert erst für ±∞ gegen 0. Aber es schadet nicht viel wenn man die Funktion abschneidet, so dass sie auf den Bereich ±2 um eine Position f herum begrenzt ist:

w_i(f) = max(0, gauss(f, mean=i, var=0.6²) - gauss(2, mean=0, var=0.6²))

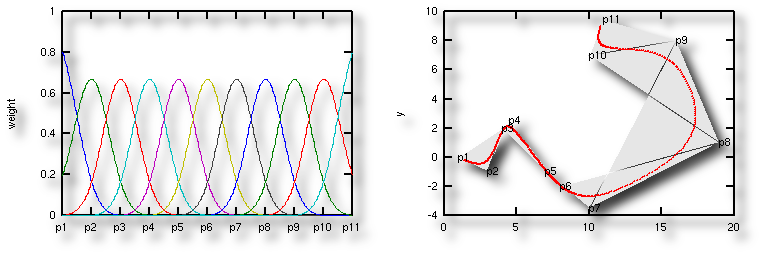Links: die normierten Gewichte, die auf einer abgeschnittenen Normalverteilungskurve beruhen
Rechts: die resultierende Kurve

Differenz
abgeschnittene zu voller Normalverteilung

Abstand korrespondierender Punkte bei Verwendung der unmodifizierten Normalverteilung (es gehen immer alle Kontrollpunkte in die Berechnung ein) zur abgeschnittenen Variante (es haben an jedem Punkt max. 4 Kontrollpunkte ein Gewicht > 0 und gehen damit in die Berechnung ein). Die Differenz (der "Fehler") ist relativ klein.

Anzumerken ist, dass die Kurve keinen der Kontrollpunkte trifft - auch den ersten bzw. letzten nicht. Man kann die Gewichte aber so modifizieren, dass die Randpunkte tatsächlich erreicht werden. Dazu darf an den Rändern des Parameterraums jeweils nur noch das Gewicht des entsprechenden Kontrollpunktes ungleich 0 sein, während alle anderen dort kein Gewicht mehr haben.

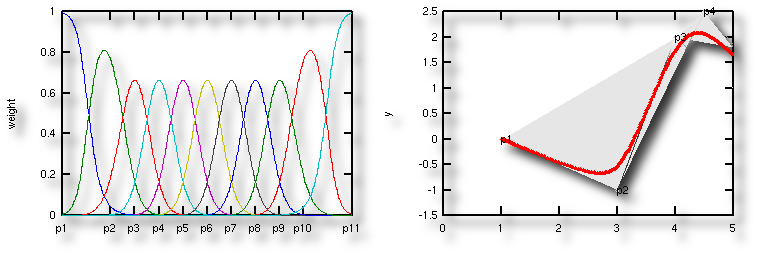
Die normierten Gewichte (links), die an den Rändern (u.a. auch über die Abstände der Punkte im Parameterraum) modifiziert wurden,
so dass die resultierende Kurve (rechts, Ausschnitt) den Anfangs- und End-Kontrollpunkt tatsächlich erreicht.

Einfacher ist es aber oft einen Punkt mehrfach einzufügen, um die Kurve dazu zu "zwingen" diesen Punkt zu treffen. Diese Methode ist auch leichter für Punkte die nicht am Rand der Kurve liegen umzusetzen. Dabei muss ein Randpunkt doppelt, andere Punkte sogar dreifach eingefügt werden, damit die Kurve einen Kontrollpunkt tatsächlich trifft.

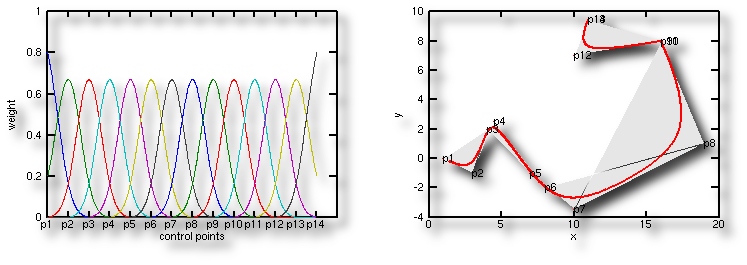
Der letzte Punkt des bisherigen Beispiels wurde doppelt (P13, P14), der drittletzte dreimal (P9, P10, P11) eingefügt. das reicht jeweils, damit ein Punkt am Rand bzw. in der Mitte tatsächlich von der Kurve getroffen wird.

Eine weitere Abwandlung besteht darin den Kontrollpunkten Gewichtsfaktoren zuzuordnen, mit denen die Gewichtsfunktionen skaliert werden. Das geht dann schon in Richtung NURBS-Freiflächen, die ich hier nicht näher behandle.
Außerdem gibt es noch geschlossene Kurven. Dabei kann man sich die Kontrollpunkte wie in einem geschlossenen Kreis vorstellen: hinter dem letzten Kontrollpunkt kommt wieder der erste und umgekehrt.

1)	Alternativ könnte man das Ganze natürlich auch mit f aus [0..N-1] definieren; wobei man es sich dann gedanklich einfacher macht, wenn man auch die Kontrollpunkte P₀..P_N-1 nennt...
2)	Die konvexe Hülle ist hier, wo über max. 4 Punkte gemittelt wird, durch die Fläche gegeben die entsteht wenn man jeweils drei aufeinander folgende Kontrollpunkte verbindet und die so entstehenden Dreiecksflächen zusammennimmt

B-Spline-Oberflächen

Ganz ähnlich werden B-Spline-Oberflächen gebildet. Nur sind die Kontrollpunkte P_i,j hier in NxM-Matrizen organisiert und haben also einen Spalten-Index i und einen Zeilen-Index j:

P = ∑_i ∑_j u_i(g) · v_j(h) · P_i,j

Dabei hängen die Spalten-Gewichte u_i von einem Parameter g aus [1...N] und die Zeilen-Gewichte v_j von einem zweiten Parameter h aus [1...M] ab (g und h ersetzen also hier den bisher einzigen Parameter f). Eine Position auf der Oberfläche ist damit eindeutig durch ein Tupel (g,h) definiert. Ansonsten ist die Berechnung identisch. Zu beachten ist, dass man für ein Segment zwischen den Punkten P_i,j, P_i+1,j, P_i+1,j+1 und P_i,j+1 jeweils nur noch die umliegenden Punkte ± eine Zeile/Spalte benötigt (da für alle anderen Punkte die Gewichte in diesem Segment 0 sind).

Um geschlossene B-Spline-Flächen zu erzeugen kann man sich jeweils jede Zeile und jede Spalte von Kontrollpunkte wie einen geschlossenen Kreis vorstellen, d.h. hinter dem letzten Punkt kommt wieder der erste der jeweiligen Spalte/Zeile. Für mich war es aber interessanter mehrere B-Spline-Flächen "sauber" zusammenfügen zu können. Dazu mehr im folgenden Unterabschnitt.

Zusammenfügen von B-Spline-Flächen

Die "Nachbarschaften" für ein Segment lassen sich auch über die Grenzen einer Fläche hinweg bestimmen, indem man umliegende Flächen, die sich Punkte an ihren Rändern teilen, mit einbezieht. Wichtig dabei ist, dass angrenzende Kontrollpunkt-Matrizen anders orientiert sein können! Randpunkte die in der einen Matrix in derselben Spalte, aber unterschiedlichen Zeilen stehen, können in der Kontrollpunktmatrix einer benachbarten Fläche in unterschiedlichen Spalten, aber dafür in derselben Zeile stehen und umgekehrt. Selbst wenn z.B. zwei Kontrollpunkte P₁ und P₂ in beiden Matrizen z.B. in jeweils einer Spalte stehen, kann es trotzdem sein, dass in der einen Matrix P₁ "über" P₂ (bezogen auf den Zeilenindex) steht in der anderen aber genau umgekehrt. Dasselbe gilt natürlich umgekehrt genauso für Punkte die in jeweils einer Zeile beider Matrizen stehen.

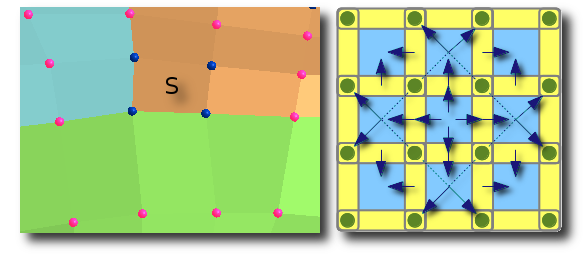Links: Um die Fläche zu einem Segment S zu berechnen, welches "zwischen" vier Kontrollpunkten liegt (hier blau) benötigt man zusätzlich noch die weiteren Nachbarn, die hier pink dargestellt sind. Diese können aber von verschiedenen Flächen stammen (hier sind es drei Flächen in den Farben: grün, blau und orange), deren Kontrollpunkt-Matrizen unterschiedlich orientiert sein können. Rechts: Schema wie benachbarte Segmente auch über Flächengrenzen gefunden werden.

Ich habe daher alle Segmente aller Kontrollpunktmatrizen in eine Struktur überführt, die von diesen Orientierungsproblemen nicht betroffen ist (man sagt auch "die der Orientierung der Matrizen gegenüber invariant ist). Dabei hat jedes Segment vier Kanten. Jede Kante ist eine Menge von zwei Punkten¹⁾. Jeder Kante sind die angrenzenden Segmente in einer Map zugeordnet (normalerweise sollten das maximal zwei Segmente je Kante sein). Ein Segment kann zudem für einen seiner Eckpunkte den diagonal gegenüberliegenden Kontrollpunkt zurückliefern. Damit kann für jedes Segment (nicht nur die an Flächengrenzen) die nötige Nachbarschaft gefunden werden:

Für jede der vier Kanten eines Segments werden die jeweils anderen Segmente gesucht, die diese Kante beinhalten
Für die beiden Punkte dieser Kante werden die jeweils diagonal gegenüberliegenden Punkte des angrenzenden Segments gesucht
Mit den nun bekannten Punkten werden die orthogonalen Kanten des angrenzenden Segments gebildet
dadurch können die noch fehlenden Eck-Segmente gesucht werden. Wenn man nun z.B. von dem oben angrenzenden und dem links angrenzenden Segment nicht dasselbe linke obere Ecksegment finden, dann hat man es mit einer "Irregularität" zu tun (Näheres dazu siehe unten)

Problematisch wird es, wenn "irreguläre" Punkte entstehen - d.h. Punkte an die mehr als vier Segmente angrenzen. Die beste Lösung, die ich bisher gefunden habe, besteht nicht darin eine Lösung zu finden, die die angrenzenden Segmente (in der unten stehenden Grafik nummeriert von 1-5) sowohl untereinander, als auch mit den angrenzenden "regulären" Segmenten "sauber" zu verbindet. Nach einer solchen Lösung habe ich zwar einige Zeit gesucht, jedoch nichts Brauchbares gefunden (siehe auch das Kapitel "Greatest Misses"). Stattdessen wird das Problem, welches sich - je nach konkreter Implementierung - z.B. in sternförmigen Löchern äußern kann, quasi nur bis zur Unsichtbarkeit verkleinert, indem die beteiligten Segmente automatisch in kleinere Segmente unterteilt werden. Dazu müssen weitere Kontrollpunkte eingefügt werden. Am einfachsten ist es, alle Segmente aller Flächen jeweils in 2x2 kleinere Segmente zu unterteilen und dieses Verfahren dann rekursiv solange zu wiederholen, bis die Segmente ausreichend klein sind, um die Irregularitäten zu "verschleiern". Allerdings erhöht man damit die Anzahl der Kontrollpunkte und Segmente natürlich dramatisch. Noch besser ist es daher, nur die Segmente entlang der Kanten die von irregulären Punkten ausgehen weiter zu unterteilen.

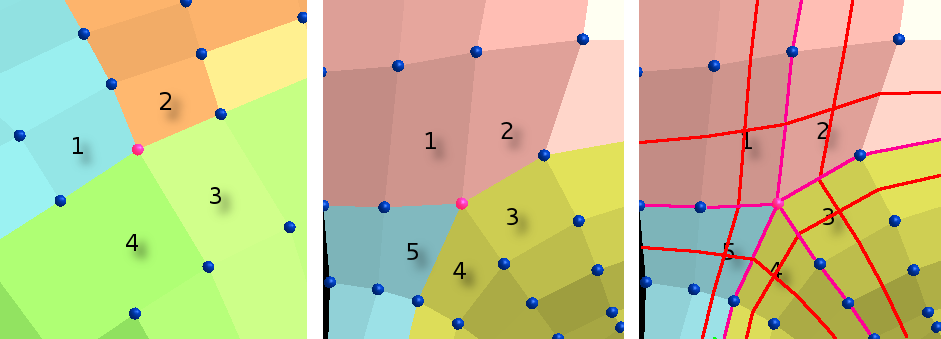Links: "reguläre" Verbindung von in diesem Fall drei Flächen: jeder Punkt gehört zu genau vier Segmenten. Mitte: Irregulärer Punkt (pink), der an insgesamt fünf Segmente von wiederum drei Flächen grenzt. Damit lässt sich die Nachbarschaft dieses Punktes nicht mehr in einer Punkt-Matrix abbilden. Rechts: Erste Unterteilung (rot) entlang der "irregulären" Kanten (pink) ausgehend von einem "irregulären" Punkt.

In jedem Fall bringt die Technik des mehrfachen Unterteilens noch ein weiteres Problem mit sich: Wenn man die neuen Kontrollpunkte dadurch gewinnt, dass man entsprechende Punkte auf der mit den aktuellen Kontrollpunkten gewonnenen B-Spline-Fläche benutzt, dann "schrumpft" die Fläche immer weiter zusammen (zieht sich immer weiter auf die konvexe Seite gekrümmter Bereiche). Dies sollte korrigiert werden, da sich das Aussehen der Oberfläche dadurch sonst zu stark verändert.
Für diese Korrektur kann z.B. ausgenutzt werden, dass sich die Kontrollpunkte (in schwarz, s.u.), die zu korrigierenden daraus gewonnenen Kontrollpunkte (rot) und die entsprechenden Punkte auf einer wiederum aus diesen Kontrollpunkten abgeleiteten zweiten Fläche/Kurve (grün) in etwa gegenüberliegen (wobei zusätzlich noch verwendet werden kann, dass die Distanz schwarz zu rot im Mittel um den Faktor 1.5 bis 2.0 höher liegt als die Distanz rot zu grün).

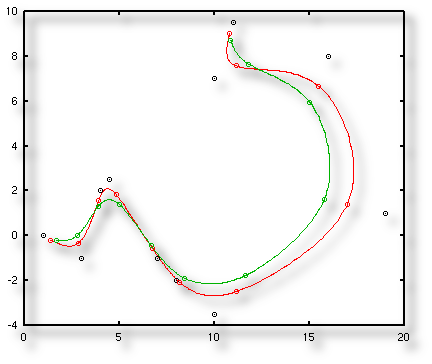
Korrektur der Kontrollpunkte: In schwarz die Kontrollpunkte; in rot die B-Spline-Kurve zu diesen Kontrollpunkten mit den Punkten, die direkt zu den Kontrollpunkten gehören; in grün die Kurve die wiederum auf den roten Kontrollpunkten basieren würde; man erkennt, dass sich grüne und schwarze Punkte bezogen auf die roten in etwa gegenüberliegen.

In der Graphik soll übrigens nur der Zusammenhang verdeutlicht werden, dass die Punkte in etwa gegenüberliegen. Praktisch erzeugt man natürlich nun aus N Kontrollpunkten (schwarz) mehr als N, also sagenwirmal z.B. M neue Kontrollpunkte (rot) und korrigiert diese dann indem man daraus weitere M "Kontrollpunkte" (grün) ableitet. Spiegelt man z.B. diese grünen an den roten Kontrollpunkten hat man die korrigierten Kontrollpunkte gefunden (einfachste Variante, ohne zusätzliche Korrektur der Abstände rot-grün). Die eigentlichen Flächen/Kurven in hoher Auflösung (hier durch rote und grüne Linien dargestellt) berechnet man in diesem Schritt noch garnicht, sondern erst ganz am Ende anhand der mehrfach weiter unterteilten und korrigierten finalen Kontrollpunkte.
Normalerweise habe ich eine hybride Methode benutzt, bei der ich zunächst alle Flächen mindestens einmal unterteilt habe und dann die Flächen entlang der "irregulären" Linien noch mehrmals weiter unterteilt wurden. Wenn man aber nur entlang der irregulären Kanten unterteilt, ohne alle Flächen mindestens einmal zu teilen, sieht man deutliche Artefakte. Diese Artefakte lassen sich aber erheblich mindern, indem man zunächst alle Punkte der oben gezeigten und beschriebenen Korrektur unterzieht, jedoch ohne dabei Flächen zu unterteilen. Erst nach dieser Korrektur wird dann entlang der irregulären Kanten weiter unterteilt (und jeweils korrigiert).

Das hier beschriebene Verfahren ist nur eine recht einfache Lösung des Problems! Bessere Varianten gibt es - dazu suche man z.B. mal nach "Catmull-Clark Subdivison" und "B-Splines" in Verbindung mit "Irregular Meshes". Solche Verfahren vereinfachen die gegebene Struktur zunächst mit dem Catmull- Clark-Verfahren. In der resultierenden Mesh-Definition hat jeder Knoten vier Kanten - jedoch kann eine Fläche weiterhin mehr oder weniger als vier Knoten/Kanten haben. Danach werden dann, je nach lokaler Mesh-Struktur, unterschiedliche "Patch-Typen" (Teilflächen-Typen) benutzt, die sich aber glatt zur Gesamtoberfläche zusammenfügen.

Zwei Mengen sind gleich wenn sie dieselben Elemente enthalten. Eine Reihenfolge der Elemente spielt dabei keine Rolle. Man kann die Kante in Java z.B. daher als 'Set' (Klasse 'HashSet') implementieren - besonders performant wäre das in dem Fall von Mengen mit jeweils genau zwei Elementen aber nicht...

Greatest Misses

Auch hier (wie schon bei meinen Versuchen mit Bezier-Flächen) gab's natürlich wieder einige - na sagen wir mal - "Irrungen und Wirrungen", wie man an den folgenden Bildern sieht. Zum Rendern der Bilder wurde natürlich auch wieder dasselbe Verfahren wie für die Fraktale verwendet - wen's interessiert der kann mal hier nachlesen. Bei den Bildern die beide Gesichtshälften zeigen sind diese übrigens tatsächlich nicht verbunden, bei denen die nur eine Hälfte zeigen wurde auch ein Modell mit nur einer Hälfte verwendet - wenigstens das ist also kein Fehler...

"Maske I" Zusammenfügen der einzelnen Segmente funktioniert noch nicht. Einige Flächen haben überhaupt noch nicht funktioniert. Und das alles, obwohl die Flächen noch nichtmal "rund" sind.	"Maske II" ...viel besser ist es noch nicht geworden...	"Maske III" ...immer noch nicht deutlich besser aber immerhin die Augen zeigen sich schonmal...	"Ecki I" Gut, alles da, noch nicht richtig verbunden, und vor allem noch eckig ("eckig" ist viel einfacher, weil man für jedes Segment nur die 4 (2x2) direkt angrenzenden Kontrollpunkte zu berücksichtigen braucht; für runde Flächen muss man dagegen eine größere Nachbarschaft heranziehen und das wiederum bedeutet, dass sich die "Einflussgebiete" überlappen)
"Maske I"	"Maske II"	"Maske III"	"Ecki I"
"Ghost I" Erster versuch die Flächen rund zu bekommen. Dafür werden für jedes Segment nicht mehr nur die vier direkt beteiligten Kontrollpunkte mit in die Berechnung einbezogen, sondern ein Raster aus 4x4 Kontrollpunkten um das jeweilige Segment (diese Raster überlappen sich also für benachbarte Segmente). Hier ist das natürlich noch grandios gescheitert...	"Ghost II" Die Flächen sind etwas größer geworden, dafür ist dem Ärmsten aber auch die Nase explodiert - also kein echter Fortschritt...	"Surreal I" ...also nochmal ein kleiner Test mit eckigen Segmenten (war schonmal besser :-)...	"Segmentist I" ...ok wir nähern uns langsam wieder...
"Ghost I"	"Ghost II"	"Surreal I"	"Segmentist I"
"Segmentist II" ...das klappt nun auch in rund, nur will da noch nicht so richtig zusammen was zusammen gehört...	"Segmentist III" ...die Abstände zwischen den Flächen sind geschrumpft, aber das prinzipielle Problem die Flächen zu verbinden ist noch nicht gelöst: An den Randsegmenten jeder Fläche müssen Kontrollpunkte aus benachbarten Flächen berücksichtigt werden, Die Kontrollpunktmatrizen angrenzender Flächen können aber beliebig anders orientiert sein...	"Grinzwanzliger Grunzwanzl" ..."kleine" Rückschläge gibt's immer wieder...	"Pesti" ...verbunden, aber nicht mehr glatt...
"Segmentist II"	"Segmentist III"	"Grinzwanzliger Grunzwanzl"	"Pesti"
"Spiderman" ...verbuchen wir es als weiteren kleinen Rückschlag (aber nett aussehen tut's immerhin)...	"Checkerman I" ...und wieder nähern wir uns...	"Checkerman II" ...kein Kommentar...	"Android" Hm, das hier scheint doch in die richtige Richtung zu gehen...
"Spiderman"	"Checkerman I"	"Checkerman II"	"Android"
"A star is born" Das hier ist erstmal die Lösung dafür mehrere Flächen, die jeweils durch eine Matrix aus Kontrollpunkten definiert sind glatt miteinander zu verbinden. Was nun aber zu Tage tritt ist das - wie sich herausstellen sollte - alles andere als triviale Problem der "irregulären" Punkte. Das sind Punkte die Teil von mehr als vier Segmenten sind (was nur an den Schnittstellen von mind. drei einzelnen Flächen vorkommen kann.	"Franz" ...nun kommt eine ganze Reihe von Versuchen die Flächen auch an den irregulären Punkten sauber zu verbinden. Das hier kann man schonmal getrost als gescheitert bezeichnen...	"Mr. trampolin man" ...ja gut, die "irregulären Punkte sind genauso (un-)sauber verbunden wie alle anderen auch, aber das war ja so nicht gewollt. Ich hatte versucht die Punkte nur anhand ihre Entfernung zu gewichten jedoch die Information über Spalten und Zeilen der Kontrollpunktematrizen zu vernachlässigen.	"Zausel" ...wie war das doch noch gleich mit den Rückschlägen?...
"A star is born"	"Franz"	"Mr trampolin man"	"Zausel"
"Terminator" Naja hier fehlen nun einfach alle Segmente, die an "irregulären" Punkten liegen.	"Ami" Da wo ursprünglich sternförmige Löcher waren sind nun sternförmige Flächen mit Löchern drumrum. Ich habe hier versucht die Flächen zu den Löchern hinzuziehen (dehnen). Abgesehen, davon dass das hier natürlich noch Mist ist, hat sich der ganze Ansatz als Irrweg entpuppt...	"Noname" Derselbe Ansatz wie eben, etwas besser ausgeführt. Was man neben den Löchern auch schon erahnen kann ist das eigentliche Problem dieser Idee: die strahlenförmig von "irregulären" Punkten nach außen gehenden Kanten (jeweils über ein Segment) lassen sich so nicht vermeiden.	"Schrotti" ...Probleme? Ich?...
"Terminator"	"Ami"	"Noname"	"Schrotti"
"Gewebe" Die Phase des hilflosen Rumprobierens...	"Knitterig" Nochmal der Versuch Kontrollpunkte nur anhand ihre Entfernung zu gewichten, jedoch nicht nach ihrer Zeilen-/Spalten-Position in der Matrix aus Kontrollpunkten einer Fläche.	"Oval" Das hier verdeutlicht das Problem: diese Bereiche sind relativ glatt, jedoch klappt die Verbindung an den Kanten nicht (wie im vorigen Bild zu sehen).	"Aalglatt" Statt das Problem zu beseitigen habe ich mich entschlossen es so klein zu machen, dass man es nicht mehr sieht - und zwar so: Es werden zusätzliche Kontrollpunkte eingefügt, so dass die Löcher um die "irregulären" Punkte so klein werden, dass man sie nicht mehr sieht. Dazu unterteile ich hier alle Segmente rekursiv mehrfach in 2x2 kleinere Segmente. Da ich diese neuen Kontrollpunkte gewinne, indem ich Punkte auf der (virtuellen) Oberfläche bestimme, die aus den Kontrollpunkten zum jeweils letzten Level resultiert, passiert Folgendes: Die Gesamtfläche "schrumpft" und wird glatter als gewünscht. Prinzipiell ist der Ansatz aber dennoch vielversprechend...
"Gewebe"	"Knitterig"	"Oval"	"Aalglatt"
"Krieger I" ...Wenn man alle Segmente aller Flächen soweit unterteilt, dass keine Löcher mehr sichtbar sind, dann bekommt man verdammt viele Segmente (Kontrollpunkte). Man könnte ja stattdessen nur die Segmente weiter unterteilen, die entlang der Kanten liegen, die von den "irregulären" Punkten ausgehen. Das hier ist der Versuch diese Segmente wenigstens erstmal zu finden und rot zu markieren, was aber noch nicht richtig funktioniert hat...	"Krieger II" ...ok Finden klappt; weiter unterteilen noch nicht wirklich...	"Android II" Hier wurden alle Segmente zur besseren Unterscheidung zufällig eingefärbt. Das Unterteilen (nur) der notwendigen Segmente funktioniert aber noch nicht korrekt (es werden teilweise die falschen Segmente bzw., die richtigen Segmente, aber in der falschen Richtung (horizontal/vertikal) unterteilt, was dazu führt, dass sie ihre Nachbarsegmente nicht finden, weil es einfach keine größenmäßig passenden Nachbarsegmente mehr gibt...	"Faltig" Soweit klappt die Unterteilung nun. Das Problem ist aber, dass die Flächen an den Stellen, wo zusätzliche Kontrollpunkte eingefügt werden anders schrumpfen als in den anderen Bereichen, wodurch Einkerbungen ("Falten") entstehen...
"Krieger I"	"Krieger II"	"Android II"	"Faltig"
"Kunterbunt" Diese Debug-Ausgabe mit zufällig eingefärbten Segmenten verdeutlicht nochmal die Unterteilung entlang bestimmter Segmentgrenzen (zu erkennen an den dort deutlich schmäleren Segmenten).	"Alt" ...und hier sehen wir schön wie man das Problem mit den Falten nicht löst... schlimmer geht's nicht? ...	"Schrumpelig" ...ohhh doch!	"Hartschale" ...immerhin: die Kanten sind kleiner geworden und der Rest ist rund...
"Kunterbunt"	"Alt"	"Schrumpelig"	"Hartschale"
"Deformant" Ich gebe zu, es ist nicht so ganz offensichtlich, aber das ist die Lösung: Die Tendenz zur Verkleinerung der Flächen durch das rekursive Unterteilen muss korrigiert werden. Nur ist das hier noch nicht so ganz gelungen...	"Finalist" ...aber hier hat die Korrektur geklappt - und zwar so: Mit den neu berechneten Kontrollpunkten (jeweils mehr als vorher), werden die zu jedem Kontrollpunkt gehörenden (Korrektur-)Punkte auf der zugehörigen Oberfläche bestimmt (diese Korrekturpunkte liegen dann noch weiter "innen"). Nun werden die Konrollpunkte in der entgegengesetzten Richtung um den Betrag der Distanz Kontrollpunkt-zu-Korrekturpunkt verschoben. Eigentlich war's das, aber...	"Explodiert" ...man könnte ja auch Bezier-Flächen automatisch in Punkt-Gitter umwandeln und auf denen dann den Algorithmus laufen lassen. Warum? Weil man damit die Kanten zwischen einzelnen Bezier-Flächen doch noch beseitigen könnte - hoff	"Bezier2BSpline" Hat geklappt! Links die Bezierflächen mit deutlich erkennbaren Kanten; rechts die zu Kontrollpunktmatrizen für B-Spline-Flächen konvertierten Flächen, die deutlich glattere Übergänge haben. Allerdings sieht man hier rechts dafür (schwach) die einzelnen Segmente. Dies lässt sich aber noch mit einer besseren Gewichtungsfunktion über die 4x4 zu berücksichtigenden Kontrollpunkte je Segment verbessern.
"Deformant"	"Finalist"	"Explodiert"	"Bezier2BSpline"
"Eierkopp" Wie's aussieht hängt natürlich auch davon ab wieviele Kontrollpunkte man je umzuwandelnder Bezier-Fläche berechnet. Hier sind es nur 4 (2x2). Ohne Korrektur der "Irregularitäten sieht's doppelt schlecht aus, aber...	"Eierkopp mit Sockenschuss" ...aber auch wenn man die Irregularitäten noch weiter verkleinern würde als hier sähe das Ergebnis deutlich anders aus als das Original (zwei Bilder vorher).	"Fliegengitter" Kein eigentlicher Fehler, sondern nur mit zu geringer Auflösung berechnet. Man sieht noch einmal sch&oum;n die Bereiche, die automatisch weiter unterteilt wurden, um die "Irregularitäten" zu verschleiern
"Eierkopp"	"Eierkopp mit Sockenschuss"	"Fliegengitter"

Ergebnis

Als "Beweis", dass das beschrieben soweit funktioniert und vor allem keine Kanten mehr erzeugt, erstmal nur das eine Bild hier. Mehr kommt noch, wenn ich Zeit habe ein ordentlicheres Gesichtsmodell zu bauen...

Texturiert Das Gesichtsmodell ist noch nicht wirklich toll, aber mit Textur sieht's schon ganz brauchbar aus. Kanten sieht man jedenfalls keine mehr - was ja das eigentliche Ziel war...		Ohne Texture Hier nochmal ohne Textur - wie gesagt nicht sooooo doll...		Gesichtsmodell Das dazugehörige Gesichtsmodell (die Flächen der rechten Gesichtshälfte wurden zur besseren Unterscheidbarkeit unterschiedlich eingefärbt)
Texturiert		Ohne Textur		Gesichtsmodell

Java-Applikation

Zum Download geht's hier

Feedback

Freue mich über eure Meinungen, Anregungen, usw.
Mail-Adresse

.
Feedback-Formular