
Wavelet Transformation (DWT)
Bestimme die neue Farbe eines Bildpunktes indem über alle benachbarten Bildpunkte bis zu einem maximalen Abstand r gemittelt wird, die zudem nicht stärker als bis zu einer maximalen Farbdifferenz d vom alten Wert des neu zu bestimmenden Bildpunktes abweichen. Man kann die Sache etwas verkomplizieren, indem nicht alle Werte gleichberechtigt in die Mittelung eingehen sondern z.B. räumlicher Abstand (in Pixeln) und/oder die Farbdifferenz zur Gewichtung genutzt werden.Ein Beispiel dafür was man mit einem selektiven Weichzeichner (hier der aus dem Programm Gimp) erreichen kann ist unten im mittleren Bild dargestellt. Obwohl das zugegebenermaßen mit einigem Parameter-Tuning noch etwas besser geht, zeigt das Verfahren die Tendenz zu sehr einheitlichen Farbflächen, die teilweise "ausfransen" (Schatten ganz rechts und Nasenrücken). Zudem wird das Bild teilweise geschärft, was manchmal ja durchaus erwünscht sein kann jedoch nicht in jedem Fall. Das Ergebnis ist oft ein etwas unnatürliches und flächiges Aussehen. Das Bild rechts zeigt diese Tendenzen nicht. Dafür hat es etwas an Kontrast und Schärfe verloren.
 |
 |
 |
| Original | Selektiver Weichzeichner | DWT-Glättung |
Das rechte Bild ist - wer hätte das gedacht - ist mit dem im Folgenden beschriebenen Verfahren geglättet worden. Das Verfahren benutzt die Diskrete Wavelet Transformation. Zu Wavelets könnte man viel schreiben, ich beschränke mich hier aber auf das was ich a) weiss und was b) unbedingt nötig ist.
|
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Potenz erweitern |
Verlängerung |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
Der Einfachheit halber gehe ich im Weiteren von der "Zweier-Potenz-Methode" aus. Entsprechend der Analyse-Levels muss das Signal in umgekehrter Reihenfolge durch Synthese-Schritte rekonstruiert werden (siehe auch Abschnitt 2-D (Multi-Level)).
|
|
||||||||
Hier wird nur der Tiefpass-Anteil weiterverarbeitet (erneut gefiltert), da aber in den Spalten (Zeilen) des zeilenweise (spaltenweise) hochpass-gefilterten Anteils auch noch Tiefpass-Information "steckt" könnte auch der Hochpass-Anteil noch einem weiteren Zerlegungs-Schritt unterzogen werden. |
||||||||
|
|
||||||||
|
 |
 |
| Original | Aus 25% der Gesamt-Information (ohne die Hochpass-Anteile der ersten beiden Levels) |
 |
 |
| Aus 12.5% der Information (ohne Levels 1 bis 3) |
Aus 6.25% der Information (ohne Levels 1 bis 4) |
"Weglassen" von Information kann man sich so vorstellen als seien alle Elemente einzelner Levels auf "0" gesetzt worden. Um noch "ansehnliche" Bilder zu erhalten darf nur die Hochpass-Information der ersten k Levels (1...k) weggelassen werden (je größer k desto unschärfer das resultierende Bild). Es ist jedoch prinzipiell möglich immer nur die Information genau eines Levels zu verwenden und so aus jedem den Beitrag zum (zu rekonstruierenden) Ausgangsbild zu errechnen. Macht man das für alle L Levels und summiert dann (pixelweise) die L resultierenden Bilder erhält man wieder das Ausgangsbild. Diese Berechnungsweise wäre zwar zur einfachen Synthese schrecklich ineffizient, jedoch ist das Verfahren für die Bild-Glättung hilfreich. Das Schema dieser Berechnung ist daher unten dargestellt:
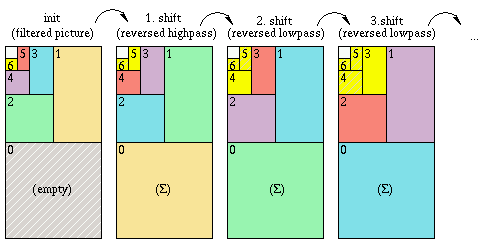 |
|
eine Farbe in der Shift-Matrix steht für einen bestimmten Informations-Anteil; um das Bild zu rekonstruieren können alle Teil-Ergebnisse direkt im Level 0 summiert werden |
Der höchste Level besteht eigentlich aus zwei Teilen: neben dem Hochpass-Anteil, gibt es noch den "restlichen" Tiefpassanteil (in obiger Grafik ist das der kleine freie Bereich jeweils links oben). Um das Ausgangsbild zu rekonstruieren müsste man also auch diesen Teil, mittels des Synthese-Tiefpass-Filters, in den Level L-1 schieben und dort die beiden Anteile aus Hoch- und Tiefpass summieren. Da hier jedoch im Weiteren nur die Hochpassinformation interessiert, wird der Tiefpass-Anteil der Information vernachlässigt (Anmerkung: wenn man die Zerlegung mittels der Analyse-Filter bis zum höchst-möglichen Level durchgeführt hat, dann besteht dieser Level L aus genau einem Pixel Tiefpass- und einem Pixel Hochpass-Anteil).
Nun wird dieses Shift-Schema solange erneut angewendet bis auch die Information aus dem Level L im Level 0 angekommen ist und dort aufsummiert wurde. Dabei müssen und dürfen im Durchlauf s nur noch die Levels 1 bis L-s+1 abgearbeitet werden (sonst würde man dieselbe Information mehrfach aus den oberen Levels holen). Wichtig ist außerdem, dass in allen weiteren Durchläufen (also alle außer dem ersten) nun der Synthese-Tiefpass-Filter verwendet wird.
Um nun Störungen vom Rest der Bildinformation trennen zu können wird zunächst eine Gewichtsmatrix w erstellt, die dann im Synthese-Schritt berücksichtigt wird. Bei dieser "gewichteten Synthese" gibt es zwei mögliche Ansätze: Bei der ersten werden die Beiträge des Levels k zum Level k-1 gewichtet, während bei der zweiten Variante das gefilterte Signal selbst gewichtet wird. Eigentlich scheint mir die erste Variante vernünftiger, tatsächlich zeigen sich aber kaum Unterschiede.
|
|
||||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||||
|
for (long ci=0; ci<n; ci++) { for (long yi=0; yi<len/2; yi++) { long xi = 2*yi-ci+offset x[t(xi)] +=y[yi]*c[ci]*w[yi];// using weights w } } |
Nun fehlt eiegntlich "nur" noch die Bestimmung der Gewichtsmatrix w selbst.
Dazu kommen wir zunächst noch einmal auf das im vorigen Kapitel erläuterte Shift-Schema und
die dort gezeigte Shift-Matrix zurück.
|
|||||||||||||||||||||||||||||||||||||||||||||||
Die Stationen der Berechnungen:
 |
 |
 |
 |
| a) Original | b) Gewichtsmatrix (Variante 1) |
c) Kumulierte Störungen (wenig Frosch, viel "Grissel") |
d) Entstörtes Bild "a) minus c)" |
Warum denn eigentlich zwei bzw. drei Shifts bei der Erstellung der Gewichtsmatrix?
Der Gedanke ist eben nicht einfach schwache Amplituden als Störung zu bewerten, sondern zu bewerten wie stark sich etwas in mehreren Levels abzeichnet. In der Variante 1 ist mindestens ein Shift notwendig, da nicht direkt die gefilterten Werte des Levels k, sondern deren Beiträge zum nächst größeren Level k-1 gewichtet werden sollen. Der nächste Shift sorgt dann in beiden Varianten dafür dass nicht die Werte eines Levels zu ihrer eigenen Gewichtung genutzt werden. Jedoch ist der k+1-te Level ja nicht in derselben Richtung (horizontal/vertikal) sondern orthogonal zum zu gewichtenden k-ten Level gefiltert worden. Daher sorgt der letzte Shift schließlich dafür dass der k+2-te Level zur Gewichtung herangezogen wird, welcher ein weiteres Mal in derselben Richtung (horizontal/vertikal) gefiltert wurde wie der k-te Level. (dass der k+2-te Level - entstanden aus dem k+1-ten Level - auch bereits einmal orthogonal dazu gefiltert worden ist stört dabei nicht weiter).Welchen Sinn hat die abgewandelte Synthese-Filterung bei der Erstellung der Gewichtsmatrix - insbesondere die Funktion h()?
Ein Datenpunkt des gefilterten Signals (auf Level k) geht bei der (normalen/gewichteten) Synthese-Filterung in mehrere Punkte des rekonstruieren Signals (des "vorigen" Levels k-1) ein. Die Berechnungsweise bei der Erstellung der Gewichtsmatrix sorgt dafür dass alle diese Beträge mindestens so hoch gewichtet werden, wie es der Amplitude im gefilterten Signal (Level k) an der entsprechenden Stelle entspricht. Dass die Gewichte dadurch einen relativ grob gerasterten Eindruck machen scheint keine negativen Auswirkungen zu haben - unerwünschte Effekte entstehen im Gegenteil bei einer "Abrundung" dieser Gewichtsmatrix (z.B. durch eine andere Funktion h'(), die nur in der "Mitte" den Wert 1 liefert und zu den Rändern hin abfällt).Wie steht's um die Glättung im Bereich "scharfer" Kanten?
Nicht so gut. Wie an der Gewichtsmatrix zu erkennen werden Bereiche um solche Kanten herum nicht bzw. weniger geglättet. Die Größe dieser Bereiche hängt von der Anzahl der Filter-Koeffizienten ab. Dadurch sind "kürzere" Filter im Vorteil. Eine Abhilfe besteht in der Möglichkeit im bei der "Kumulation der Störungen" z.B. im ersten Shift nicht die gewichtete sondern die normale Synthese-Filterung zu verwenden. Dadurch verliert das Bild aber logischer Weise auch an Schärfe, denn im ersten Shift wird so alle Information als Störung aufgefasst. Die besten Ergebnisse werden erreicht, wenn diese Bereiche mit Hilfe eines Selektiven Weichzeichners (da ist er wieder :-) nachbearbeitet werden, wobei die Gewichte der Gewichtsmatrix bestimmen wo und wie stark nachgeglättet werden darf. Im einfachsten Fall verwendet man nur die Gewichte des Levels 0, noch besser - aber auch noch aufwändiger - ist eine erneute Analyse- / Synthese-Filterung des entstörten Bildes, wobei im Synthese-Schritt auf jedes Zwischenergebnis der Selektive Weichzeichner unter Beachtung der jeweiligen Gewichte für diesen Level angewendet wird. Bei mehr als zwei Filterungs-Levels erhält man zwar sehr "glatte" aber keine natürlich wirkenden Ergebnisse mehr (siehe unten).Gibt's irgendwelche Seiteneffekte?
DWT-Glättung +
Selektiver Weichzeichner
angewendet auf Levels 0 und 1DWT-Glättung +
Selektiver Weichzeichner
angewendet auf Levels 0-3DWT-Glättung +
Selektiver Weichzeichner
angewendet auf Levels 0-7
Die Bilder haben im (normalen) Jpeg-Format z.B. mit 75%-er Qualität teilweise nur noch 50% des Speicherbedarfs - hängt aber sehr von der Stärke der Störungen ab.
 |
 |
|
Gleichmäßige
Störungen
/
harte
Kontraste
|
nicht
optimale Glättung an einigen Kanten (vom integrierten selektiven Weichzeichner nachgebessert) |
 |
 |
| starkes
Farbrauschen |
dafür recht homogenes Resultat |
 |
 |
| Gleichmäßige
Störungen |
leichte
Einbußen
in
der
Schärfe, keine Glättung an harten Kanten (z.B. Zähne) |
 |
 |
| starke
vertikale
Störung mit hohem Kontrast |
DWT-Glättung
ist
ein
Kompromiss aus Glättung und Erhalt der Schärfe |
 |
 |
| beim
Selektiven Weichzeichner subjektiv höhere Schärfe aber auch etwas unruhiger |
Das Differenzbild
zeigt deutliche Unterschiede in der Entstörung sowie großflächigere Helligkeitsunterschiede |
 |
 |
 |
 |
| relativ
schwache
horizontale
Störungen...
|
...wurden praktisch ohne Einbußen entfernt... | ...das
kann
z.B.
der
Selektive
Weichzeichner aber auch... |
...das
Differenzbild offenbart entsprechend praktisch nur
Helligkeitsunterschiede |
Alle Bilder wurden mit dem Debauchy-9/7-Filter bearbeitet. Die Werte für den (einzigen) Glättungs-Parameter level90 lagen bei 128 bzw. 196. Die Bilder sind in Originalgröße dargestellt (d.h. der Größe in der sie auch gefiltert wurden).
Deutlich besser als z.B. beim selektiven Weichzeichner werden die Ergebnisse meiner Beobachtung nach oft bei sehr großen Bildern, wie man sie z.B. beim Scannen von Dias oder Negativen erhält. Dabei kann man dann (den mühsam eingebauten) selektiven Weichzeichner auch teilweise ganz ausschalten, da hier die DWT-Glättung alleine schon sehr gut funktioniert. Derartig große Bilder kann ich hier jedoch leider nicht darstellen...
|
Analyse-Tiefpass-Filter-Koeffizenten: |
Analyse-Hochpass-Filter-Koeffizenten: |
|
|
|
. | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
Analyse-Tiefpass-Filter-Koeffizenten: |
Analyse-Hochpass-Filter-Koeffizenten: |
|
|
|
. | |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|








 .
.