Die Problematik und die relativ einfache vorgestellte Methodik eignen sich recht gut um einige Grundbegriffe einzuführen. Das ist der eigentliche Gedanke hinter dieser Seite - weniger die Entwicklung eines "optimalen" OCR-Systems.

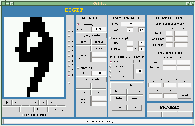
Los geht's... Angenommen man hat einen Datensatz einzelner Muster (Pattern) die sich wiederum aus binären Werten zusammensetzen. Als Beispiel nehmen wir einen Datensatz handgeschriebener Ziffern, wobei jede Ziffer in einer Matrix mit Breite x Höhe-Bildpunkten (Pixeln) abgelegt ist. Diese Pixel sind entweder schwarz (Wert=1) oder weiß (Wert=0). Um dies zu erreichen müssen die handgeschriebenen Ziffern normalerweise zunächst eingescannt und dann einer geeigneten Vorverarbeitung (z.B. Kontrastverstärkung) unterzogen werden, wobei auch die Auflösung auf ein geeignetes Maß reduziert wird (hier wurde mit 16 x 16 Pixeln gearbeitet). Weiterhin sei zu jeder Ziffer bekannt welche der Zahlen 0-9 sie darstellen soll, d.h. die Muster lassen sich in die Klassen 1 bis 10 einteilen. Der Einfachheit halber stehe die Klasse 1 für die Ziffer "1", Klasse 2 für "2", ... und Klasse 10 für die "0".  

Datensatz Muster ... ... ... ... ... ... Bedeutung "1" "1" "1" ... "2" "2" "2" ... "3" "3" ... "4" ... "5" ... "9" "9" ... "0" "0" "0" Klasse (Nr) 1 1 1 ... 2 2 2 ... 3 3 ... 4 ... 5 ... 9 9 ... 10 10 10

Mit Hilfe dieser Beispiel-Muster soll nun versucht werden andere handgeschriebene Ziffern zu klassifizieren, d.h. es soll automatisch erkannt werden ob es sich um eine "1", eine "2", etc. handelt. Dazu soll ein Programm mit den Beispiel-Mustern (Trainings-Mustern) derart trainiert werden, dass es die Aufgabe mit einer möglichst geringen Fehlerrate absolviert. Die einfachste Möglichkeit ein Muster zu klassifizieren besteht darin es mit allen bekannten Beispiel-Mustern zu vergleichen und es bei einer vollkommenen Übereinstimmung derselben Klasse wie das Beispiel-Muster zuzuordnen. Damit könnten alle Beispiel-Muster richtig klassifiziert werden, d.h. der Trainingsfehler läge bei 0%. Die Beispiel-Muster werden natürlich nur zu Testzwecken klassifiziert, denn die richtige Klasse ist ja bekannt. Die eigentliche Aufgabe ist es neue Muster zu klassifizieren. Es ist jedoch (bei vernünftiger Bildauflösung) höchst unwahrscheinlich, dass zwei Muster Pixel für Pixel exakt übereinstimmen (bei 16x16 binären Pixeln gibt es theoretisch 2^(16*16) = 1e77 mögliche Muster). Neue Muster können daher mit diesem Ansatz nicht klassifiziert werden, das System wäre nicht in der Lage z.B. die generellen Merkmale einer "1" zu extrahieren, um jede "1" auch als solche zu erkennen. Ein solches System kann nicht generalisieren - der Generalisierungsfehler läge bei (fast) 100%.  

Klassifikation Eingabe-Muster  (Klasse unbekannt)   Progamm   Klassifikationsergebnis "9"

Statt alle Pixel eines neuen Musters mit allen entsprechenden Pixeln der Trainings-Muster zu vergleichen, könnte man nur einige Pixel (z.B. die Pixel B-I F-II und C-VII, s. Abb. "Pattern") zum Vergleich heranziehen. Anhand weniger Pixel lassen sich die Ziffern der Trainings-Daten aber normalerweise nicht eindeutig unterscheiden. Angenommen das zu klassifizierende Muster hat die Werte 0,1,1 für die zu vergleichenden Ziffern. Nun ist es möglich und sogar ziemlich wahrscheinlich, dass mehrere Beispiel-Muster verschiedener Klassen dieselben Werte für diese Vergleichs-Pixel aufweisen. Das System könnte also in der Regel nicht zwischen verschiedenen Klassen unterscheiden, weil die Komplexität des Systems zu gering ist um die zur Differenzierung notwendigen Eigenschaften zu lernen. Ein solches System "leidet" unter underfitting, entsprechend nennt man die vorher erörterte Überanpassung an die Beispiel-Muster overfitting.  

Klassifikation mit einem Look-Up-Table Pattern (8x8)   A B C D E F G H   I   1               II           2       III                   IV                   V                   VI                   VII     3             VIII                                       LUT 1 - Eingangs-Pattern LUT-Eingangsdimension: 1 2 3   Pixel-Koodrinaten: B-I F-II C-VII   Aktueller Wert: 0 1 1     C-VII C-VII C-VII   LUT 1     Eingangs-Pattern Summe   Votum Votum       000 001 010 011 100 101 110 111 (probabilistic) Klasse 1       0         N1 0 0 / S011 / N1 * N / K 2       2         N2 1 2 / S011 / N2 * N / K 3       3         N3 1 3 / S011 / N3 * N / K ... ... ... ... ... ... K       0         NK 0 0 / S011 / NK * N / K       Anzahl (Summe) S000 S001 S010 S011 S100 S101 S110 S111 N ? 1   (S001=0+2+3+...+0)   (probabilistic) (0/0:=1/K)

Die Methode nur wenige Vergleichs-Pixel zu benutzen hat dennoch einen Vorteil: Die zur Klassifizierung benötigten Daten lassen sich in einem Look-Up-Table (LUT) ablegen. So können bei drei Pixeln nur die 8 Kombinationen (000), (001), (010), (011), (100), (101), (110) und (111) auftreten. In einer Tabelle mit diesen 8 Kombinationsmöglichkeiten als Spaltenüberschriften und den 10 Klassen als Zeilenbeschriftung (s. Abb. LUT1) lässt sich jedes Trainings-Muster genau einer Zelle in der Tabelle zuordnen. In den Zellen werden die Anzahlen der entsprechenden Trainings-Muster aufsummiert. Es kann damit schnell das "Votum" des LUT's zu einem neuen Muster ermittelt werden. Alle Klassen zu denen bezüglich der Vergleichspixel identische Beispiel-Muster existieren (d.h. deren Zellen Werte >0 haben) sind möglich. Eine Erweiterung besteht darin die genauen Anzahlen zu berücksichtigen, indem höhere Anzahlen entsprechend stärker für die betreffende Klasse sprechen. Dieser hier als "probabilistisch" (probabilistic) bezeichnete Ansatz setzt in dieser Form jedoch voraus, dass zu jeder Klasse etwa gleich viele Trainings-Muster existieren. Der Effekt, dass natürlicher Weise mehr Übereinstimmungen mit den Beispielen einer Klasse zu erwarten sind, zu der auch mehr Beispiel-Muster existieren, kann jedoch berücksichtigt werden (s. Abb. LUT1 Spalte "Votum (probabilistic)").
Damit ist jedoch noch keine ausreichende Lösung gefunden. Um zu brauchbaren Ergebnissen zu gelangen können nun mehrere (viele) LUT's aufgestellt werden, die ein Muster jeweils anhand verschiedener Vergleichs-Pixel betrachten. Jedes LUT votiert dann für die aus seiner Sicht möglichen Klassen (im Mode "probabilistic" mit unterschiedlichen Gewichten für die möglichen Klassen). Die Klasse für die die meisten Stimmen eingegangen sind wird als Klassifikations-Ergebnis ausgegeben.  

Klassifikation mit mehreren LUT's     Votum LUT1 Votum LUT2 Votum LUT3 ... Summe Klassifi- kation Klasse 1 0 1 0   11   2 1 1 0   13 3 1 0 1   5 4 1 0 0   1 5 0 0 1   7 6 0 1 1   12 7 1 0 0   8 8 1 1 0   15 (max) 9 0 0 0   3   10 0 0 0   6

Um zu bestimmen wie gut ein solches System ist muss der Generalisierungsfehler geschätzt werden. Im Unterschied zu vielen anderen Verfahren liegt der Trainingsfehler bei einer ausreichenden LUT-Anzahl i.d.R. bei 0%, so dass aus dem Trainingsfehler nicht mal mit der allgemein gebotenen Vorsicht auf den Generalisierungsfehler geschlossen werden kann. Eine Möglichkeit zur Bestimmung des Generalisierungsfehler besteht aber darin die verfügbaren Daten in Trainings- und Test-Daten aufzuteilen. Die Test-Daten werden nicht zum Trainieren des Systems genutzt. Der Test-Fehler den das System nach dem Training mit den Trainings-Daten auf den Test-Daten macht ist ein gutes Maß für den Generalisierungsfehler. Leider wird so aber ein größerer Teil der Daten "verschenkt" - kann nicht zum Training genutzt werden. Die Cross-Validation-Methode teilt die Daten daher mehrfach unterschiedlich auf. Es wird jweils nur ein sehr kleiner Teil der Daten als Test-Datensatz abgespalten und der Rest zum Treining verwendet. Danach wird ein anderer Test-Datensatz abgespalten und das Training mit den neuen Trainingsdaten wiederholt. Der Gesamt-Test-Fehler aller Durchläufe ist ebenfalls ein gutes Maß für den Generalisierungsfehler. Jedoch geht jeweils nur ein sehr kleiner Teil der Daten für das Training verloren. Im hier vorgestellten Ansatz ist es sogar besonders leicht möglich jeweils nur ein einziges Trainings-Muster aus den Trainingsdaten zu entfernen (Leave-One-Out-Cross-Validation), da das "Verlernen" eines Beispiel-Musters mit der Subtraktion einer 1 in der betreffenden Zelle jedes LUT's zu bewerkstelligen ist. Bei anderen Verfahren (z.B. Neuronalen Netzen) ist dagegen oft ein erneutes längeres Training für jede unterschiedliche Trainings-Menge erforderlich.

Die Optimierung eines solchen Systems wirft mehrere Fragen auf:
Eine Frage ist vieviele Pixel pro LUT als Vergleichspixel benutzt werden sollen. Diese Frage hängt mit der Anzahl der Trainings-Muster zusammen. Je größer der Datensatz umso mehr Vergleichspixel pro LUT sind möglich.

Eine weitere Frage betrifft die Auswahl der Vergleichs-Pixel eines LUT's.

• Die einfachte Möglichkeit besteht darin die Pixel zufällig aus dem gesamten Pattern auszuwählen.
• Eine weitere Möglichkeit ist die Vergleichs-Pixel eines LUT's lokal zu begrenzen, d.h. sie nur innerhalb eines Rezeptiven Felds (RF) von Rm x Rn Bildpunkten zufällig auszuwählen (Unterschiedliche LUT's haben dann natürlich unterschiedliche RF's, so dass das gesamte Muster abgedeckt wird).

Die dritte offensichtliche Frage ist wieviele LUT's benutzt werden sollen. Es ist i.d.R. so, dass sich die Ergebnisse (gemessen am Generalisierungsfehler) mit der Anzahl verwendeter LUT's verbessern. Die größere LUT-Anzahl erhöht aber auch Rechen- und Speicherbedarf. Es ist daher sinnvoll zu versuchen die Anzahl der LUT's zu reduzieren, indem die Pixel-Auswahl optimiert wird. Beide oben beschriebenen Methoden können mit Optimierungsverfahren kombiniert werden. Dazu werden um jeweils ein LUT zu erzeugen, zunächst mehrere Test-LUT's erzeugt, bewertet und alle bis auf das beste wieder verworfen. Es gibt verschiedene Bewertungskriterien (Informationskriterien): CV-Fehler-Optimierung: Es wird das LUT gewählt, dass zusammen mit den schon fest bestimmten LUT's den geringsten CV-Fehler bewirkt. Problematisch ist, dass damit die Aussagekraft des CV-Fehlers bezüglich des Generalisierungsfehlers sinkt, da dieser direkt zur Optimierung herangezogen wird.
  COGENTROPY (COmputing GENeralization using enTROPY, [1]) Die Anzahl kritischer Beispiele ki wird für jedes der N Trainings-Beispiel bestimmt. Das ist die Menge von Trainings-Mustern die mindestens entfernt ("verlernt") werden muss um eine Fehlklassifikation dieses Trainings-Beispiels im CV-Test zu bewirken. Die Entropie ist definiert als:

-H = (N-k1) log (N-k1) + ... + (N-kN) log (N-kN)

Die Anzahl kritischer Beispiele ist schwierig zu bestimmen. Als Abschätzung kann folgendes Verfahren benutzt werden: Bei der (korrekten) Klassifikation eines Musters gibt es (mind.) eine konkurrierende zweitbeste Klasse. Der Stimmenunterschied zwischen der richtigen und dieser konkurrierenden Klasse betrage n Stimmen. Um eine Fehlklassifikation zu erreichen müssen mindestens n LUT's nicht mehr für die richtige Klasse stimmen. Sortiert man die LUT's nach den Differenzen der Muster-Anzahlen dj zwischen den beiden Klassen, so ergibt sich ein LUT mit der n-kleinsten Differenz dn.  Es gilt:

d1+ ... dn <= ki <= dn

Da auch hier der CV-Test zur Optimierung herangezogen wird besteht prinzipiell das gleiche Problem wie bei der ersten Methode. Zusätzlich können auch noch Hemmungsgewichte benutzt werden. Die Idee dahinter ist, dass bestimmte LUT's durch ihre spezielle Vergleichs-Pixel-Auswahl bestimmte Klassen besonders gut unterscheiden können.  Das Verfahren ist dieses:

1. Finden aller Trainingsbeispiele, die falsch oder nur knapp richtig erkannt wurden (CV-Test).
2. Feststellen der "konkurrierenden" Klasse(n) für jedes dieser Trainingsbeispiele
3. Finden aller LUT-Spalten, die für die richtige Klasse aber nicht für die konkurrierende(n) (falschen) Klasse(n) stimmen (entsprechende Zellen haben den Wert 0).
4. Speichern eines Hemmungs-Faktors a<0 in diesen Zellen der konkurrierenden Klasse(n) (typisch: a=-10/#LUT's)

Die Hemmungsfaktoren summieren sich nur dann zu relevanten Größen, wenn ein LUT sehr oft die betreffenden Klassen unterscheiden kann.
Auch hier spielt der CV-Test wieder eine Rolle, so dass der CV-Fehler letztlich deutlicher den tatsächlichen Generalisierungsfehler unterschätzen wird.

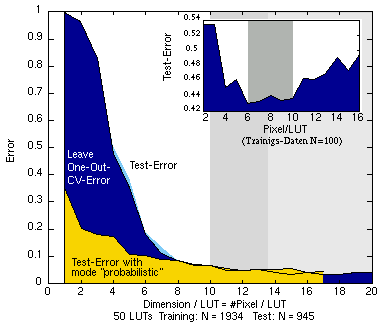Kleines Bild: Test-Fehler bei (nur) 100 Trainings-Mustern; der kleinste Test-Fehler ergibt sich für 6-10 Vergleich-Pixel pro LUT, davor ist das Modell nicht in der Lage die relevanten Eigenschaften zu lernen (underfitting) danach beginnt eine Überanpassung an die Trainings-Daten (overfitting) Großes Bild: 1934 Trainings-Muster, 945 Test-Muster; der CV-Fehler ist ein gutes Maß für den Test-Fehler (Generalisierungsfehler), der probabilistische Modus bring Vorteile bei weniger Vergleichspixeln pro LUT, bei höheren Eingangsdimensionen jedoch Nachteile. Der geringste Fehler wird erreicht wenn mindestens 10 Vergleichs-Pixel pro LUT verwendet werden (Beginn des overfittings hier erst bei >20 Pixeln/LUT)

 
 

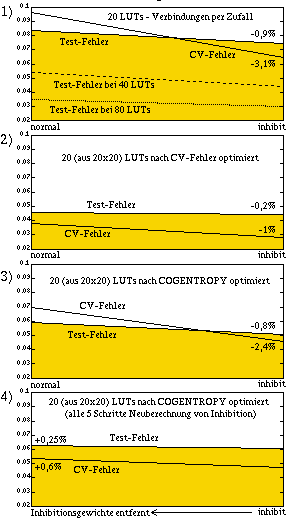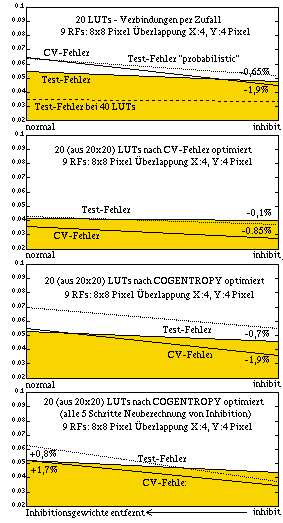Vergleich verschiedener Verfahren:  links: jedes LUT kann Pixel aus dem gesamten Muster verwenden;  rechts: die Pixel eines LUT sind innerhalb rezeptiver Felder lokal eingeschränkt; jeder Graph stellt jeweils den Fehler mit ("inhibit") und ohne Hemmungsgewichte ("normal") dar.  Zu erkennen ist fast immer, dass der CV-Fehler durch Hemmungsgewichte stärker fällt als der Test-Fehler, da die Cross-Validation bei der Hemmungsgewichts-Bestimmung schon zum Finden der falsch / nur knapp richtig klassifizierten Muster benutzt wurde.

 
 
 

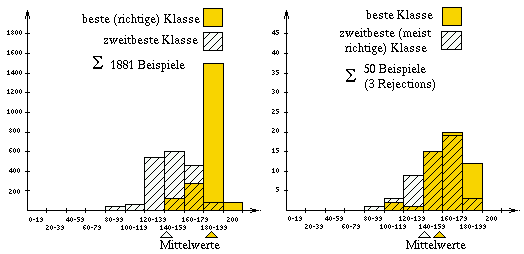Vergleich der bestbewerteten Klasse (Klassifikationsergebnis) mit der zweitbesten Klasse für richtig klassifizierte Muster (links) und falsch klassifizierte Muster (rechts); die X-Achse gibt die Anzahl der Stimmen (LUT's) an, die Y-Achse gibt die Anzahl der Fälle an. (System: 200 LUT's, Daten: 1934 Muster, Test-Verfahren: CV-Test)

[1] "Classification Of Handwritten Digits Using A RAM Neural Net Architecture",  Thomas Martini Jorgensen